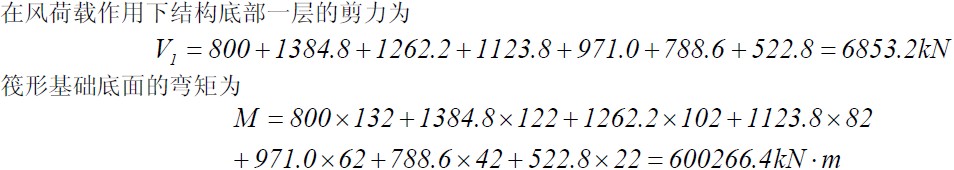3.2 风荷载
  空气从气压大的地方向气压小的地方流动就形成了风，与建筑物有关的是靠近地面的流动风，简称为近地风。当风遇到建筑物时在其表面上所产生的压力或吸力即为建筑物的风荷载。风荷载的大小及其分布非常复杂，除与风速、风向有关外，还与建筑物的高度、形状、表面状况、周围环境等因素有关，一般可通过实测或风洞试验来确定。对于高层建筑，一方面风使建筑物受到一个基本上比较稳定的风压，另一方面风又使建筑物产生风力振动，因此，高层建筑不仅要考虑风的静力作用，还要考虑风的动力作用。                       
3.2.1 风荷载标准值
   主体结构计算时，垂直于建筑物表面的风荷载标准值wk应按式（3.2.1）计算，风荷载作用面积应取垂直于风向的最大投影面积。                                                                a

   1. 基本风压
   当气流以一定的速度向前运动，遇到建筑物的阻塞时，就形成高压气幕，从而对建筑物表面产生风压。根据风速，可以求出风压，但是风速随高度、周围地貌的不同而不同，为了比较不同地区风速或风压的大小，必须对不同地区的地貌，测量风速的高度有所规定。按规定地貌和高度等条件所确定的风压称为基本风压，我国《荷载规范》规定，基本风压系以当地比较空旷平坦地面上离地10m高统计所得的50年一遇10分钟平均最大风速v0（m/s）为标准，按w0=160020v确定的风压值，应按《荷载规范》中全国基本风压分布图及有关数据采用，但不得小于0.3kN/m2。对于特别重要或对风荷载比较敏感的高层建筑，基本风压应适当提高，应按100年重现期的风压值采用，《荷载规范》规定有100年重现期的风压值，可直接查取。
   2. 风压高度变化系数
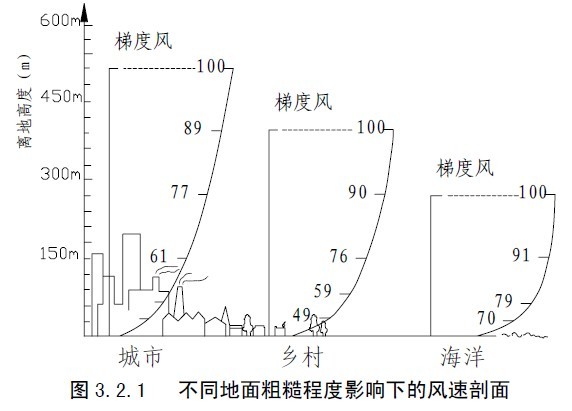
   由于地表对风引起的摩擦作用，使接近地表的风速随着离地表距离的减小而降低。只有在距离地表300—500m以上的高空，风速才不受地表的影响，能够在气压梯度的作用下自由流动，达到所谓梯度速度，将出现这种速度的高度称为梯度风高度。地表粗糙度不同，近地面风速变化的快慢也不相同。图3.2.1给出了不同地貌下平均风速沿高度的变化规律。由图可知，地面越粗糙，风速变化越慢，梯度风高度将越高；反之，地表越平坦，风速变化越快，梯度风高度将越小。如开阔乡村和海面的风速比高楼林立大城市的风速更快地达到梯度风速；或位于同一高度处的风速，城市中心处要比乡村和海面处小。风压沿高度的变化规律一般用指数函数表示： ()αHzvvHz= （3.2.2）
   式中 、——分别为任意点高度及该处的平均风速； zzv
   H、——分别为标准高度（例如10m）及该处的平均风速； Hv
   α——地面粗糙度系数；地表粗糙程度愈大，α值则愈大；通常，海面取0.100—0.125；开阔平原取0.125—0.167；森林或街道取0.250；城市中心取0.333。 由          

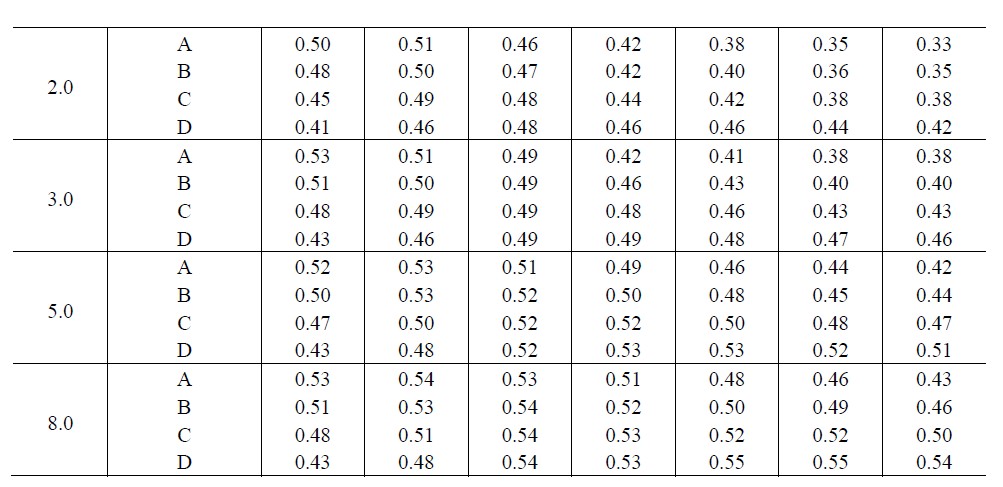
a              由于《荷载规范》仅给出了高度为10m处的风压值，即基本风压，所以其他高度处的风压应根据基本风压乘以风压高度变化系数0wzμ换算得来，即风压高度变化系数定义为某类地表上空高度处的风压与基本风压的比值，该系数取决于地面粗糙程度指数zzw0wα。现行《荷载规范》将地面粗糙程度分为A，B，C，D四类：
梯度风梯度风海洋乡村城市70799110049597690100617789100梯度风离地高度（m）
图3.2.1 不同地面粗糙程度影响下的风速剖面
A类——指近海海面、海岛、海岸、湖岸及沙漠地区；
B类——指田野、乡村、丛林、丘陵以及房屋比较稀疏的乡镇和城市郊区；
C类——指有密集建筑群的城市市区；
D类——指密集建筑群且房屋较高的城市市区。
  相应的粗糙度指数α分别为：A类取0.12；B类取0.16；C类取0.22；D类取0.30。对应于不同地面粗糙程度时的梯度风高度分别为：A类为300m；B类为350m；C类为400m；D类为450m。
以B类地面粗糙程度作为标准地貌，其梯度风高度为，地面粗糙程度系数为0tH0α；任意地貌（如地面粗糙程度为A类，B类，C类，D类）的相应值为、αtHα，根据梯度风高度的定义可得

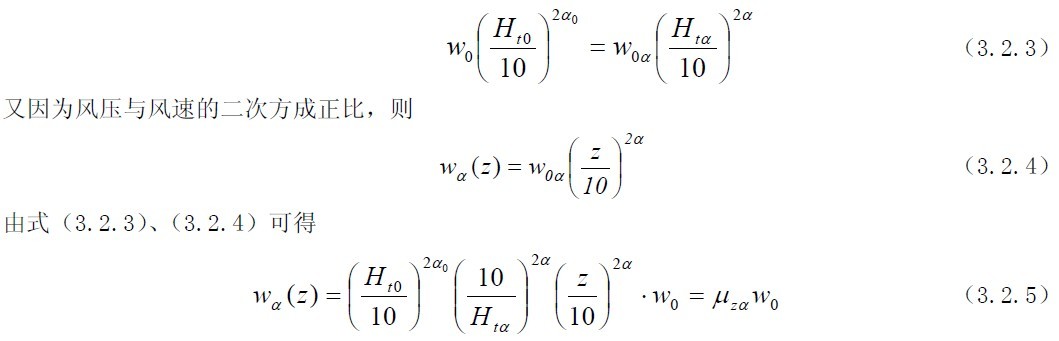a 将各种地貌情况下的梯度风高度和地面粗糙程度系数代入式（3.2.5），可求得A、B、C、D四类风压高度变化系数为a        根据上式可求得各类地面粗糙程度下的风压高度变化系数，如表3.2.1所示。

a    3. 风荷载体型系数
   当风流动经过建筑物时，由于房屋本身并非理想地使原来的自由气流停滞，而是让气流以不同的方式从房屋表面绕过，从而风对建筑物不同的部位会产生不同的效果，有压力，也有吸力，空气流动还会产生漩涡，对建筑物局部会产生较大的压力或吸力。风压实测表明，即使在同样的风速条件下，建筑物表面上的风压分布是很不均匀的，一般取决于房屋的体型、尺寸等几何性质有关。图3.2.2为一矩形建筑物的实测结果，图中风压分布系数是指房屋表面风雅分布系数，正值是压力，负值是吸力。图3.2.2（a）为房屋平面风压分布系数，表明当风流经建筑物时，在迎风面上产生压力，在侧风面及背风面均产生吸力，而且各面风压分布并不均匀；图3.2.2（b）为迎风面和背风面的风压分布系数，即风等压线。表明在建筑物表面上的某个部分风压力（或吸力）较大，另一些部分较小，风压分布也并不均匀。通常，迎风面的风压力在建筑物的中间偏上为最大，两边及底下最小；侧风面一般近侧大，远侧小，分布也极不均匀；背风面一般两边略大，中间小。

a     风荷载体型系数是指风作用在建筑物表面所引起的压力(吸力)与原始风速算得的理论风压的比值。风荷载体型系数一般都是通过实测或风洞模拟试验的方法确定，它表示建筑物表面在稳定风压作用下的静态压力分布规律，主要与建筑物的体型与尺度有关。在计算风荷载对建筑物的整体作用时，只需按各个表面的平均风压计算，即采用各个表面的平均风荷载体型系数计算。根据我国多年设计经验及风洞试验，高层建筑风荷载体型系数可按下列规定采用：
  （1）单体风压体型系数
  根据国内外风洞试验资料，可得出风压体型系数sμ在各个面上的分布。《高层规程》规定如下：
  ① 圆形平面建筑取0.8；
  ② 正多边形及截角三角形平面建筑，按下式计算： ns2.18.0+=μ （3.2.7）
  式中： n为多边形的边数；
  ③ 高宽比H/B不大于4的矩形、方型、十字形平面建筑取1.3；
  ④ 下列建筑取1.4：
  1）V形、Y形、弧型、双十字形、井字形平面建筑；
  2）L形、槽形和高宽比H/B大于4的十字形平面建筑；
  3）高宽比H/B大于4，长宽比L/B不大于1.5的矩形、鼓形平面建筑。
  ⑤ 迎风面积取垂直于风向的最大投影面积。
  ⑥ 在需要更细致进行风荷载计算的情况下，可按附表1采用，或由风洞试验确定。
  ⑦ 当房屋高度大于200m时宜采用风洞试验来确定建筑物的风荷载。对于建筑平面形状不规则，立面形状复杂；立面开洞或连体建筑；周围地形和环境较复杂的高层建筑，当高度大于150m时宜由风洞试验确定建筑物的风荷载。在对复杂体型的高层建筑结构进行内力和位移计算时，正反两个方向风荷载的绝对值可按两个中的较大值采用。
  （2）群体风压体型系数
  对建筑群，尤其是高层建筑群，当房屋相互间距较近时，由于漩涡的相互干扰，房屋某些部位的局部风压会显著增大。为此，《高层规程》规定，当多栋或群集的高层建筑相互间距较近时，宜考虑风力相互干扰的群体效应。一般可将单体建筑的体型系数sμ乘以相互干扰增大系数，该系数可参考类似条件的试验资料确定，必要时宜通过风洞试验确定。
  （3）局部风压体型系数
  在计算风荷载对建筑物某个局部表面的作用时，要采用局部风荷载体型系数，用于验算表面围护结构及玻璃等强度和构件连接强度。
  檐口、雨蓬、遮阳板、阳台等水平构件计算局部上浮风荷载时，风荷载体型系数sμ不宜小于2.0。设计建筑幕墙时，应按有关的标准规定采用。
  4. 风振系数
  风对建筑物的作用是不规则的，风压随风速、风向的紊乱变化而不停地改变。图3.2.3（a）所示为实测的风速时程曲线。由图可看出，风速的变化可分为两部分：一种是长周期的成分，其值一般在10min以上；另一种是短周期成分，一般只有几秒左右。因此，为便于分析，通常把实际风分解为平均风（稳定风）和脉动风两部分。由于平均风的长周期远大于一般结构的自振周期，因此这部分风

a   对结构的动力影响很小可以忽略，可将其等效为静力作用，使建筑物产生一定的侧移。而脉动风周期较短，与一些工程结构的自振周期较接近，且其强度随时间随机变化，其作用性质是动力的，使建筑物在平均风压产生的侧移附近左右振动，如图3.2.3（b）所示。对于高度较大，刚度较小的高层建筑，波动风压会产生不可忽略的动力效应，在设计中必须考虑。目前采用加大风荷载的办法来考虑这个动力效应，即对风压值乘以风振系数。
  对于基本自振周期大于0.25s的工程结构，以及高度大于30m且高宽比大于1.5的高柔房屋均应考虑脉动风压对结构产生的风振影响。当房屋高度大于30m、高宽比大于1.5且可忽略扭转影响的高层建筑，均可仅考虑第一振型的影响。结构在z高度处的风振系数1Tzβ可按下式计算： zzz 1μ?υξβ+= （3.2.8）
  式中：ξ―脉动增大系数，可按表3.2.2采用；
  υ―脉动影响系数，外形、质量沿高度比较均匀的结构可根据结构总高度H及其与迎风面宽度B的比值按表3.2.3采用；
  z―振型系数，可由结构动力计算确定，计算时可仅考虑受力方向基本振型的影响；对于质量和刚度沿高度分布比较均匀的弯剪型结构，也可近似采用振型计算点距室外地面高度与房屋高度zH的比值，即HHi/z=，为第i层标高；H为建筑总高度。iH
  在按表3.2.2确定脉动增大系数时，结构基本自振周期可由结构动力学计算确定。对比较规则的高层建筑结构，也可采用近似公式计算：钢结构 nT)15.0~10.0(1=
  钢筋混凝土框架结构 nT)1.0~08.0(1=
  钢筋混凝土框架-剪力墙和框架-核心筒结构 nT)08.0~06.0(1=
  钢筋混凝土剪力墙结构和筒中筒结构 nT)06.0~05.0(1=
  或 钢筋混凝土框架和框剪结构 32311053.025.0BHT?×+=
  钢筋混凝土剪力墙结构 3103.003.0BHT+=
  式中：为结构层数；nH为房屋总高度（ｍ）；B为房屋宽度（ｍ）。

aa   3.2.2 总风荷载
   在结构设计时，应计算在总风荷载作用下结构产生的内力和位移。总风荷载为建筑物各个表面上承受风力的合力，是沿建筑物高度变化的线荷载。通常按x、y两个互相垂直的方向分别计算总风荷载。高度处的总风荷载标准值按下式计算： z)coscoscos(2221110nnsnsszzzBBBwWαμαμαμμβ+++=K （3.2.9）式中：为建筑物外围表面数（每一个平面作为一个表面）；、、K、为个表面的宽度；n1B2BnBn1sμ、2sμ、K、snμ为n个表面的平均风荷载体型系数；1α、2α、K、nα为个表面法线与风作用方向的夹角。
  当建筑物某个表面与风力作用方向垂直时，即，则这个表面的风压全部计入总风荷载；当某个表面与风力作用方向平行时，即，则这个表面的风压不计入总风荷载；其他与风作用方向成某一夹角的表面，都应计入该表面上压力在风作用方向的分力，在计算时要特别注意区别是风压力还是风吸力，以便作矢量相加。00=iα090=iα
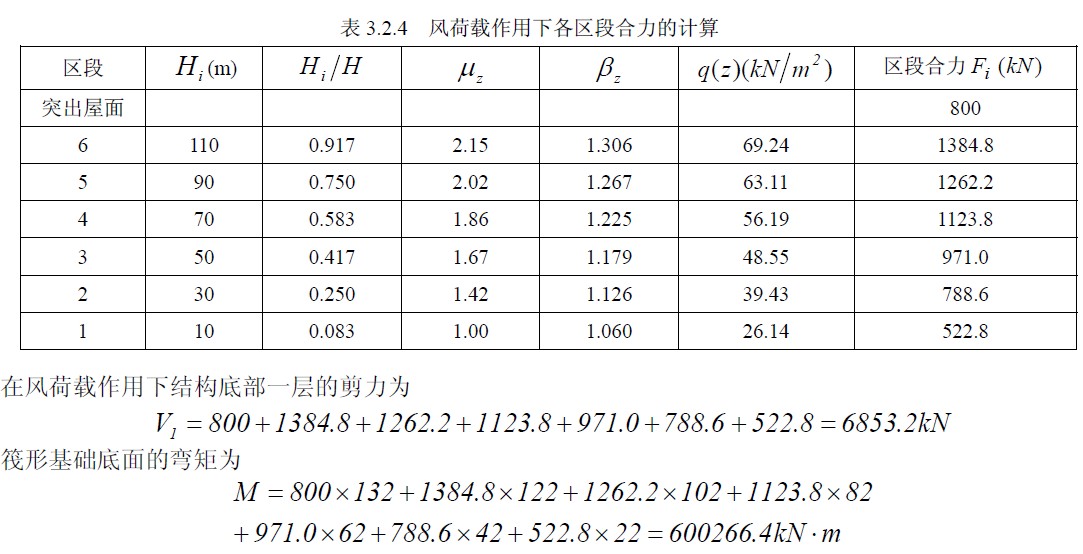
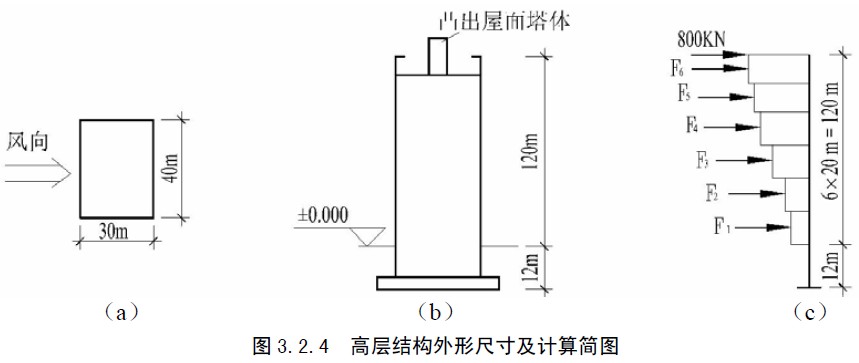
  各表面风荷载的合力作用点，即总风荷载作用点，其位置按静力平衡条件确定。                 [例题] 某高层建筑剪力墙结构，上部结构为38层，底部1-3层层高为4m,其他各层层高为3m，室外 地面至檐口的高度为120m，平面尺寸为mm4030×，地下室采用筏形基础，埋置深度为12m，如图3.2.4(a)、(b)所示。已知基本风压为2045.0mkNw=，建筑场地位于大城市郊区。已计算求得作用于突出屋面小塔楼上的风荷载标准值的总值为800。为简化计算，将建筑物沿高度划分为六个区段，每个区段为20m，近似取其中点位置的风荷载作为该区段的平均值，计算在风荷载作用下结构底部（一层）的剪力和筏形基础底面的弯矩。

aa   （3）风振系数：由条件可知地面粗糙度类别为B类，由表3.2.2可查得脉动增大系数502.1=ξ。脉动影响系数ν根据H/B和建筑总高度H由表3.2.3确定，其中B为迎风面的房屋宽度，由H/B=3.0可从表3.2.3经插值求得=ν0.478；由于结构属于质量和刚度沿高度分布比较均匀的弯剪型结构，可近似采用振型计算点距室外地面高度与房屋高度zH的比值，即HHi/z=?，为第i层标高；H为建筑总高度。则由式 （3.2.8）可求得风振系数为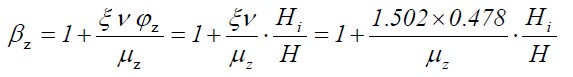：       （4）风荷载计算：风荷载作用下，按式（3.2.1）可得沿房屋高度分布的风荷载标准值为：（4）风荷载计算：风荷载作用下，按式（3.2.1）可得沿房屋高度分布的风荷载标准值为：按上述公式可求得各区段中点处的风荷载标准值及各区段的合力见表3.2.4，如图3.2.4(c)所示。