第二节 货币时间价值计算中的几个特殊问题
一、不等额的系列收付款的价值
    假设A0为第0年末的付款，A1为第1年末的付款，A2为第2年末的付款， · · ·An为第n年末的付款，则其现值计算公式为：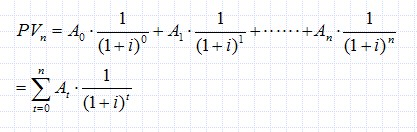
二、年金和不等额现金流混合情况下的现值这种情况又称为混合现金流。计算的方法是能用年金公式计算的部分用年金公式计算，不能用年金公式计算的部分用复利公式计算，然后把它们加总，即可以得到混合现金流的现值。见下表：三、名义年利率和实际年利率当计息期短于一年或每年复利次数超过一次，而给定的利率又是年利率时，涉及到名义年利率和实际年利率问题。给定的年利率为名义利率，而对名义利率按每年计息期长短等因素进行调整后的利率为实际利率。设r为名义利率，i为实际利率，m为每年复利的次数，则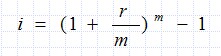：或不计算实际利率，而是调整有关指标，即利率=r/m，年数=mn
四、贴现率的确定
   根据已知条件算出终值或现值系数，然后查终值或现值系数表，找出所对应的期限中最接近的两个系数，这两个最接近的系数所属的利率值，就是要求的贴现率的近似值。最后用插值法求出贴现率。
五、72法则
    在没有计算器或系数表时，用72法则可以帮助我们计算终值。该法则认为：现值翻一倍的时间大致等于72除以年利率再乘以100，即：当年利率为10%时，你的投资大致7.2年翻一倍。假如开始投资1000元，7.2年后你将拥有2000元，14.4年后拥有4000元，21.6年后拥有8000元。
六、贷款的分期偿还
    在抵押贷款、消费贷款和特种商业贷款中，分期付款很普遍。例：按12%的年利率贷款2.2万美元，要求在6年内还清，求年偿还额。
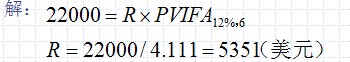注意：随着时间的推移，分期偿付额中利息偿付所占的比重是下降的，而本金所占的比重则是上升的。利息与本金之间此消彼长的关系是很重要的，因为在纳税时，只有利息才能作为费用扣除。