第二节 投资风险价值的计算
一、风险报酬（风险价值）
风险报酬或风险价值是进行风险性投资而获得的超过货币时间价值的报酬。表示方法：
（1）风险报酬额：指投资者因冒风险进行投资而获得的超过时间价值的那部分额外报酬额。
（2）风险报酬率：是风险报酬额与原始投资额的比率。
财务管理中的风险报酬常用风险报酬率来表示。
二、用概率分布衡量风险报酬
（一）单项资产的风险报酬
1、确定概率分布：概率是用来表示随机事件发生的可能性大小的数据。通常，把必然发生事件的概率定为1,把不可能发生事件的概率定为0，随机事件的概率为0—1之间。
例：某公司有两项投资机会，甲机会是一个高科技项目，该领域竞争激烈；乙机会是生产老产品而且是必需品。假设未来的经济情况只有三种：繁荣、正常、衰退，有关的概率分布和预期报酬见下表：
在不考虑通货膨胀的情况下，投资报酬率等于时间价值率与风险价值率之和。货币的时间价值率是无风险的最低报酬率。时间价值和风险报酬是财务管理中的两个基本概念。某公司甲、乙两项投资机会的概率分布及预期报酬率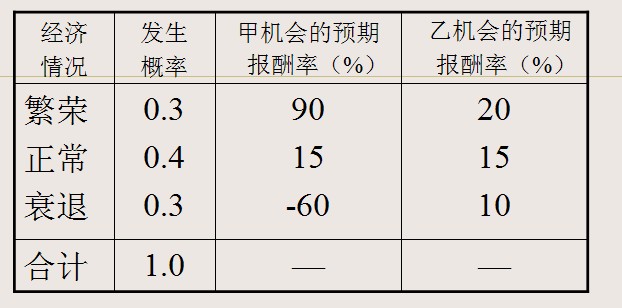
依据以上资料可以画出甲、乙两机会的概率分布图（即可以画出离散型分布图，又可以画出连续型分布图）。从图示中可以看出，报酬率的概率呈正态分布。
2、计算期望报酬率
期望报酬率：是各种可能的报酬率按其概率进行加权平均而得到的报酬率，是反映集中趋势的一种度量。
—期望报酬率； n—可能结果的个数；
Pi—第i种可能结果的概率；
ki—第i种可能结果的报酬率。
上例中 ，甲的期望报酬率=15%
乙的期望报酬率=15%
两者的期望报酬率相同，但风险不同。
3、计算标准离差：
标准离差是各种可能的报酬率偏离期望报酬率的综合差异，是反映离散程度的一种度量。收益率的标准离差越大，则收益率的分散程度越大，投资风险也越大。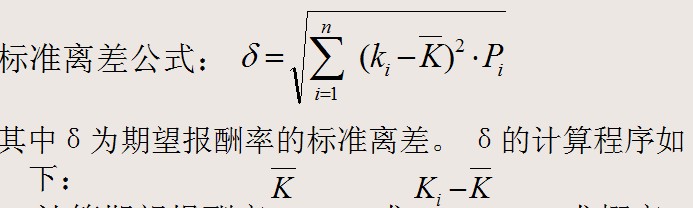
(1)计算期望报酬率 ；(2)求概率分布的方差，即将每一 差异平方再乘以与其相关的概率，并把这些乘积加总；(3)对每一方差开方，得到标准离差。
甲、乙的投资报酬率相等，因此需要根据δ来比较风险程度，则必须通过计算标准离差率才能比较风险程度。5、计算风险报酬率
风险报酬率（RR)=b·v
b—风险报酬系数，是将标准离差率转化为风险报酬的一种系数；
投资的总报酬率
K —投资报酬率；
RF—无风险报酬率,指加上通货膨胀贴水后的货币时间价值,西方一般把投资于国库券的利率视为无风险报酬率.假设甲投资机会的风险报酬系数为5%，乙投资机会的风险报酬系数为为8%，则两者的风险报酬率分别为：
RR(甲)=19.36%
RR(乙)=2.06%以上例子说明投资风险应该与反映风险程度的标准离差成正比，即所冒的风险程度越大，得到的收益率也应该越高。确定风险报酬系数的方法有以下几种：
A、根据以往的同类项目加以确定。必须在历史资料较充分的情况下采用。
B、由企业领导或企业组织有关专家确定。
C、由国家有关部门组织专家确定。
（二）证券组合的风险报酬
证券组合投资：投资者同时把资金投放于多种证券，称为证券组合投资。
1、证券组合的风险
按照是否可以分散，证券组合的风险分为可分散风险和不可分散风险两种。其中可分散风险可以通过持有证券的多样化来抵消。而不可分散风险则不可能通过证券组合分散掉，即使投资者持有的是收益水平及变动情况相当分散的证券组合，也将遭受这种风险。假设某公司所购股票W和M构成一种证券组合，每种股票各占50%，它们的报酬率和风险情况见下表：
某证券组合的报酬率和风险情况
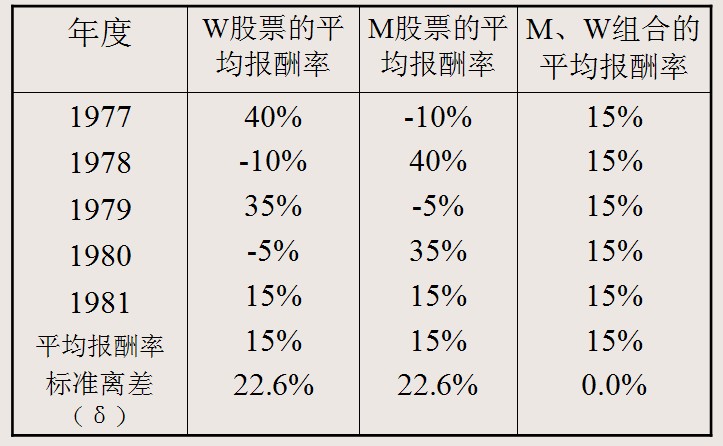
根据上表的资料，绘制出两种股票及其证券组合的报酬率图：
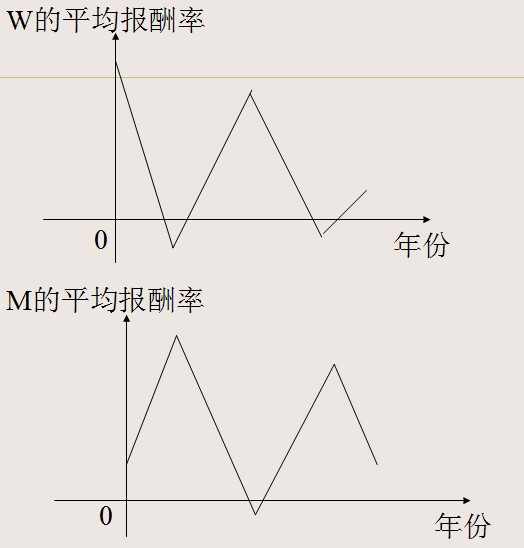
根据以上两图，可以绘制出证券组合的报酬率图
W股票和M股票都有很大的风险，但它们组合起来，则没有风险，这是因为两种股票的收益率是完全负相关，其相关系数为 –1.0。若两种股票的报酬率完全正相关，即其相关系数为+1.0，则这两种股票组成的证券组合不能抵消风险。若两种股票的相关系数为0，两股票不相关。
一般而言，随机选取两种股票，其相关系数为+0.6左右的居多。在此情况下，把两种股票或证券加以组合有可能抵减风险，但不能全部抵消。若股票种类较多，则能分散掉大部分风险。
对于不可分散风险，是无法通过证券组合分散的。但这种风险对不同企业、不同证券有不同的影响，因此也需要加以考察。通常由一些机构定期公布这种风险的大小，用β系数来衡量。
β系数是一种系统风险指数，用于衡量个别收益率的变动对于市场组合收益率变动的关联程度，即相对于市场全部资产的平均风险水平来说，一项资产所含的系统风险的大小。
组合的β系数是组合中各股β的加权平均数。
美国有关公司1995年的β系数表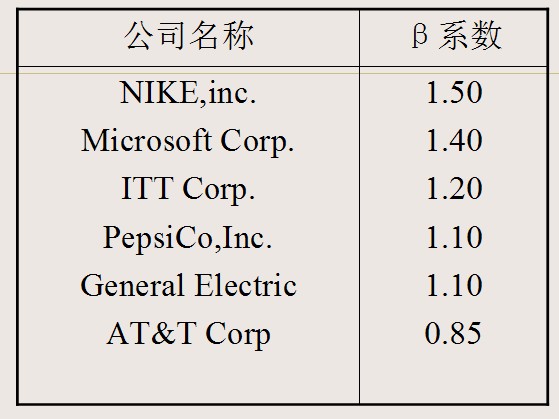
如果某种股票的β系数大于1，说明其风险高于整个市场的风险。否则，低于市场风险。证券组合的β系数公式如下：
总结：
1)证券投资的风险由可分散风险和不可分散风险两部分构成。
2)可分散风险可以通过证券组合来消除。可分散风险随证券组合中证券数量的增加而减少。
3)不可分散风险不能通过证券组合来消除，但可以通过考察β系数来了解风险的大小。2、证券组合的风险报酬：是指投资者因承担不可分散风险而要求的超过时间价值的那部分额外报酬。3、证券组合的风险
1)两项资产构成的资产组合的风险：
资产组合风险的程度由标准差来确定。假设资产1和资产2的期望收益率为R1和R2，标准差分别为δ1和δ,两种资产的相关系数是ρ12，则组合的标准差公式为：
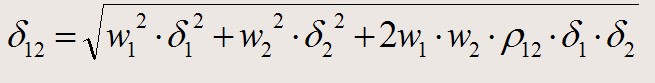W1—资产1在资产组合中所占的价值比例；
W2—资产2在资产组合中所占的价值比例；
资产组合的期望收益与资产间的相关关系无关；而资产组合的标准差的大小则与相关系数的大小有关。2)多项资产构成的资产组合的风险：
对一个由多项资产构成的资产组合，其期望收益与标准差的计算与两项资产组成的资产组合完全相同，计算公式如下：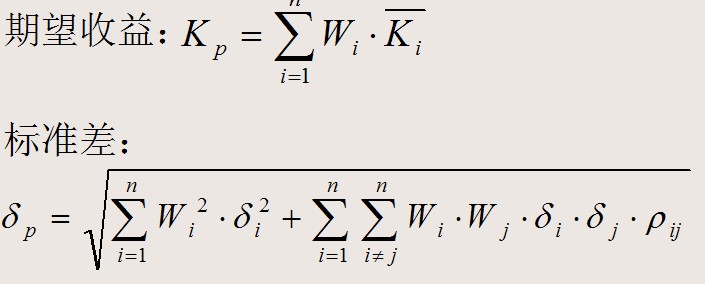
（三）风险和报酬率的关系
1、概述
确定性等值(Certainty Equivalent,CE)：某人在一定时点所要求的确定的现金额。此人认为该现金额与在同一时间点预期收到的一个有风险的金额无差别。
确定性等值<期望值，属于风险厌恶型；
确定性等值=期望值，属于风险中立型；
确定性等值>期望值，属于风险爱好型。
在市场均衡时一种证券被假定能提供与系统风险相称的期望收益率。证券的系统风险越大，投资者的期望收益率越高，期望收益率与系统风险的关系及证券的定价是资本资产定价模型的精髓。
2、资本资产定价模型（Capital Asset Pricing Model,CAPM）：
1)含义：是一种描述风险与期望收益率之间关系的模型。在这一模型中，某种证券的期望收益率是无风险收益率加上这种证券的系统风险溢价（指确定性等值和投资期望值之间的差额，是为了使投资者接受风险所必须给他的额外期望收益）。该模型产生于20世纪60年代，由1990年诺贝尔经济学奖获得者马柯维兹和夏普等人提出。
2)该模型的两个假设：资本市场是有效的；投资者对单个证券的预期相同。
3)该模型的公式表示法：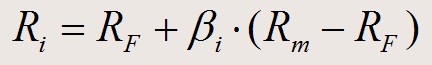
Ri：第i种证券或第i种证券组合的期望报酬率；
RF：无风险报酬率；
βi：第i种股票或第i种证券组合的β系数；
Rm：所有股票的平均报酬率或市场组合的期望报酬率。3)资本资产定价模型的图形表示法：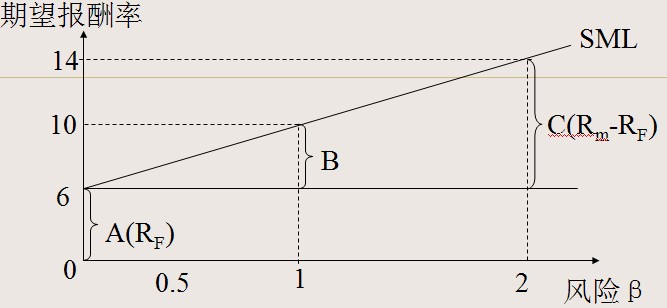 
A：无风险报酬率；B：中风险股票的风险报酬率；C：高风险股票的风险报酬率；
SML：证券市场线，表明期望报酬率与不可分散风险之间的关系。