第二节 相关分析及应用
通常两个变量之间若存在一一对应的确定关系,则称两者之间存在着函数关系。当两个随机变量之间具有某种关系时,随着一个变量数值的确定 ,另一变量却可能取许多不同值,但取值有一定的概率统计规律,这时称两个随机变量存在着相关关系。变量x 和y 之间的相关程度常用相关系数ρxy 表示
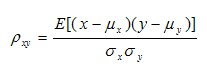
μx— 随机变量 x 的均值 μx = E [ x ]
μy— 随机变量 y 的均值 μy = E [ y ]
σx— 随机变量 x 的标准差 σ2x=E [ (x –μx )2 ]
σy— 随机变量 y 的标准差 σ2y=E [ (y –μy )2 ]
根据柯西—许瓦兹不等式可知
当数据点分布越接近于一条直线时,ρxy 的绝对值越接近1,x 和y 的线性相关性程度越好,将这样的数据回归成直线才越有意义。ρxy 的正付号表示一变量随另一变量增加而增加或减少。当ρxy 接近零时,则认为x 和y之间完全无关。但仍可能存在某种非线性的相关关系甚至函数关系。
假如 x(t) 是某各态历经随机过程的一个样本记录。x(t+τ) 是x(t) 时移τ 后的样本。在任何t =t0 时刻,从两个样本上分别得到两个量值x(ti) 和 x(ti+τ),而且它们具有相同的均值和标准差。
假如把
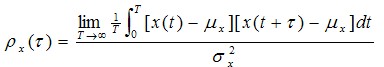
经化简得到 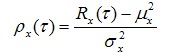
定义各态历经随机信号自相关函数为
![]()
自相关函数性质:
(1) ![]()
(2)自相关函数在τ= 0时为最大值,并等于该随机信号的均方差 ψ2x 。
(3)当τ足够大或τ→∞时,x(t)和x(t+τ)不存在内在联系,彼此无关。
(4)自相关函数为偶函数,即 ![]()
(5)周期函数的自相关函数仍为同频率的周期函数,其幅值与原周期信号幅值有关,而丢失了原信号的相位信息。
例5-1求正弦函数 x (t) = x0 sin (ωt+φ)的自相关函数。初相角φ为一随机变量。
解:此正弦函数是一个零均值的各态历经随机过程,其平均值可用一个周期内平均值表示。该函数的自相关函数为:
![]()
可见正弦函数的自相关函数是一个余弦函数,在τ=0时具有最大值,它不随τ的增加而衰减至零。保留了原正弦信号的幅值和频率信息,而丢失了相位信息。
三.信号的互相关函数
两个各态历经随机过程的随机信号 x(t)和 y(t)的互相关函数 Rxy(τ)定义为
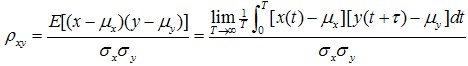
Rxy(τ)最大变动量范围为![]()
如果x(t)和y(t)两信号是同频率的周期信号或者包含有同频率的周期成分,那么,即使 τ→∞, 互相关函数也不收敛并出现该频率的周期成分如果两信号含有频率不等的周期成分,则两者不相。
结论: 同频率相关,不同频率不相关。
相关滤波:例如在线性系统中 测振。根据频率保持性,只有和激振频率相同的成分才能 是由激振而引起的响应,而其它成分是干扰。因此将激振信号与所测得的响应信号进行互相关(τ=0不用时移),就可得到由激振引起的响应幅值和相位幅值,消除了噪声干扰的影响 。这种处理方法叫相关滤波。