本节要研究汽车直线驱动行驶时,整车会受到哪些与行驶方向相同(即,切向)的外力。如果该力向前,则是驱动力;如果向后,则是行驶阻力。
汽车的车速、爬坡和加速能力,都与驱动力和行驶阻力有关。
一、 汽车的驱动力
很显然,对汽车来说,驱动力只能来自路面给驱动轮的推力。而该力的来源是发动机输出的动力。
发动机输出转矩
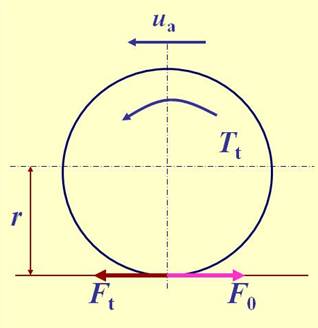
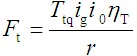 。可见,
。可见,下面依次讨论各参数:
1. 发动机的转速特性
所谓“转速特性”,就是发动机转矩、功率(以及燃油消耗率)等工作参数随转速变化的规律。
分析动力性问题时,力求动力最大化,就要利用发动机的“外特性”,即发动机节气门全开(或者高压油泵在最大供油量位置)状况下的转速特性。
如下图,就是一款典型汽油机的外特性曲线。
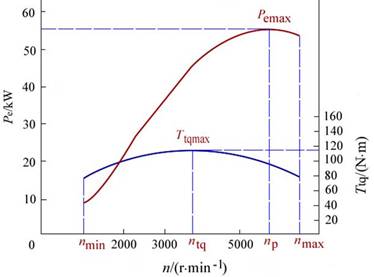
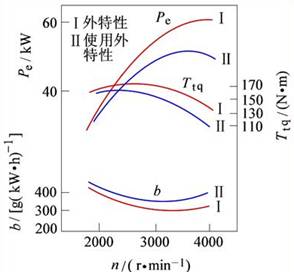
另外,带上全部附件设备时的发动机特性曲线,称为使用外特性曲线(见下图)。由于扣除了附件的消耗,使用外特性的输出比外特性略小。
而在初步分析动力性时,不必过多考虑二者的区别,统称“外特性”。
传动系统的机械效率
传动效率
VYMR.jpg)
3. 车轮半径
车轮处于不同的工况,以及分析目的不同,其半径有三个不同的定义。
自由半径:车轮处于无载时的半径。显然正常行驶的车轮不会有自由半径。
静力半径
滚动半径
严格来说,进行动力学分析要利用静力半径,进行运动学分析要利用滚动半径。但对于一般性分析来说,常不计二者的区别而统称车轮半径r。
4. 汽车的驱动力图
已论证,汽车的驱动力和发动机的转矩之间存在
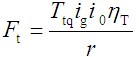 ,而简
,而简单的运动分析又可得知汽车的速度和发动机转速之间存在
QZ$4_{5N_V.jpg) 。
。(其中,车速单位为km/h,转速单位为转/分钟。)
则可将驱动力和车速的关系,按不同挡位画在同一张坐标上,得到汽车的驱动力图:
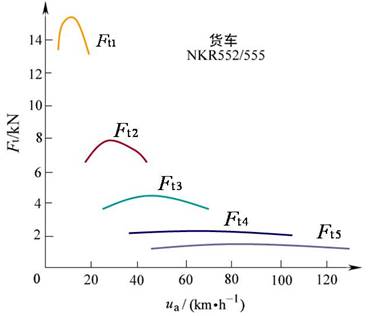
二、 汽车的行驶阻力
汽车的行驶阻力分别来自轮胎在路面上滚动时的滚动阻力
1. 滚动阻力
首先必须明确的是,滚动阻力的产生机理是由于橡胶材料的变形、而不是轮胎表面相对于地面的摩擦,所以正规称呼是“滚动阻力”、而不是“滚动摩擦”。
橡胶材料(或者其他弹性材料)自身都有“弹性迟滞”,即,相同的变形量下,压缩时的弹力大、复原时的弹力小。如图所示:
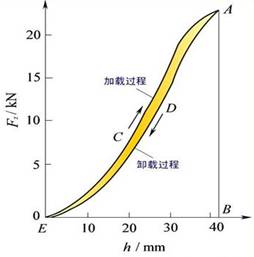
因此,当此材料制成的轮胎在路面上连续滚动时,必然要求外界不断输入能量补偿弹性迟滞的能量损失,也就是体现为一个“滚动阻力”。
滚动阻力的详细受力分析是比较繁琐的,而且驱动轮和从动轮的受力关系也不同。但是其定量计算很简单:无论对于驱动轮还是从动轮,受到的滚动阻力都是
对于整车,则有
f是滚动阻力系数,G是整车的重力。
滚动阻力系数f与轮胎结构、气压、道路状况和车速等有关。一般性分析时,认为f仅取决于道路状况。在常见的沥青或混凝土路面上,滚动阻力系数f大致在0.01-0.02之间。
2. 空气阻力
汽车直线行驶时受到的空气作用力在行驶方向的分力称为空气阻力。
空气阻力的构成和机理分析比较复杂,涉及到空气动力学知识和车身几何设计。这里不详细介绍。
在定量计算中,其大小为
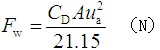 ,其中
,其中A—迎风面积(m2);
Ua—汽车速度(km/h);
可见,减小迎风面积和降低空气阻力系数,有助于减小空气阻力,是汽车车身设计的重要任务。
3. 坡度阻力
坡度阻力Fi就是重力沿坡道向下的分量,很显然Fi=Gsinα。
SLZ}}W`$QS3C9.jpg)
4. 加速阻力
汽车加速行驶时,克服其质量加速运动时的惯性力,就是加速阻力Fj。
汽车加速时,不仅平移质量(即整车质量)要加速,而且旋转质量(主要是车轮和发动机飞轮)也要加速,所以加速阻力比整车平移质量的惯性力要大。为此,引入旋转质量换算系数δ来计算加速阻力:
其中,m—汽车质量(kg)
旋转质量换算系数
T`UCC]52M2.jpg) ,
,即旋转质量换算系数δ取决于飞轮的转动惯量
三、 汽车行驶方程式
将“驱动力=行驶阻力”展开,即得到汽车行驶方程式:
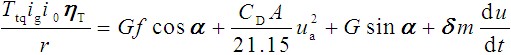
UU}_3IZ58{II.jpg)