第十二讲 极限存在的判别法Ⅱ

准则II  单调有界数列必有极限.

    如果数列{x n}满足条件

x 1£x 2£x 3£ × × × £x n£x n+1£ × × ×,

就称数列{x n}是单调增加的;  如果数列{x n}满足条件

x 1³x 2³x 3³ × × × ³x n³x n+1³ × × ×,

就称数列{x n}是单调减少的. 单调增加和单调减少数列统称为单调数列.

    如果数列{x n}满足条件x n£x n+1, nÎN+, 

    现在准则II表明：果数列不仅有界, 并且是单调的, 那么这数列的极限必定存在, 也就是这数列一定收敛.

    根据准则II, 可以证明极限存在.

    设, 现证明数列{xn}是单调有界的.

    按牛顿二项公式, 有

      , 

        . 

比较x n ,  x n+1的展开式, 可以看出除前两项外, x n的每一项都小于x n+1的对应项, 并且x n+1还多了最后一项, 其值大于0, 因此

        x n < x n+1 , 

这就是说数列{xn}是单调有界的.

    这个数列同时还是有界的.因为xn的展开式中各项括号内的数用较大的数1代替, 得

        .

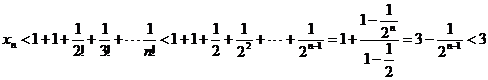根据准则II, 数列{xn}必有极限.这个极限我们用e 来表示.即

.

    我们还可以证明.e是个无理数, 它的值是

e=2. 718281828459045× × ×.

指数函数y=e x 以及对数函数y=ln x 中的底 就是这个常数.

    在极限中, 只要a(x)是无穷小, 就有

.

    这是因为, 令, 则u ®¥, 于是.

, (a(x)®0).

例1 .

    解 令t=-x, 则x ®¥时, t ®¥.于是

        .

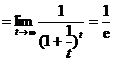或    .

例2求下列函数的极限

（1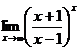）；     （2）.

分析 利用重要极限.

解 （1）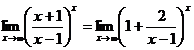

.

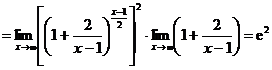（2）.