第十三讲 无穷小的比较

在极限的运算法则中，我们讨论了两个基本点无穷小的和、差及乘积仍是无穷小.那末两个无穷小的商的情况又如何呢？为此讨论下列极限.尽管都是时的无穷小量，但是它们趋向于零的快慢程度不一样.

设，是当时的两个无穷小量，由极限的运算法则知：，，都是当时的无穷小量.

 但当时是否是无穷小量呢？

 ，，，当时都是无穷小量，，，，.

1.定义

设，，

   （1）如果，就说是比高阶的无穷小，记作；

   （2）如果，就说是比低阶的无穷小；

   （3）如果，就说是与同阶的无穷小；

   （4）如果，就说与是等价无穷小，记作.

 2．等价无穷小的重要性质

定理6设 , ,且存在，则=.

   注：在计算极限的过程中，可将分子或分母的的乘积因子换为与其等价的无穷小，这种替换有时可简化计算，但注意在加、减运算中不能用.

3．常用的等价无穷小替换

：，，，，，；

   ，.

例 

注意 利用等价无穷小代换时，只有整个分子（或分母）或其因子才能用等价无穷小代换，加减运算的每一项不能代换，不能将用代换.

解 

当时，，利用等价无穷小代换有

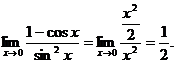从而