第十八讲 闭区间上连续函数的性质

最大值与最小值: 对于在区间I上有定义的函数f(x), 如果有x0ÎI, 使得对于任一xÎI都有

f(x)£ f(x0 )  (f(x)³f(x0 )), 

则称f(x0 )是函数f(x)在区间I上的最大值（最小值）.

例如, 函数f(x)=1+sin x在区间[0, 2p]上有最大值2和最小值0.

  定理1（最大值和最小值定理）在闭区间上连续的函数在该区间上一定能取得它的最大值和最小值.

    定理1说明, 如果函数f(x)在闭区间[a, b]上连续, 那么至少有一点x1Î[a, b], 使f(x1)是f(x)在[a, b]上的最大值, 又至少有一点x 2Î[a, b], 使f(x 2)是f(x)在[a, b]上的最小值.

    注意： 如果函数在开区间内连续, 或函数在闭区间上有间断点, 那么函数在该区间上就不一定有最大值或最小值.

    定理2（有界性定理）在闭区间上连续的函数一定在该区间上有界.

    零点： 如果x0 使f(x0 )=0, 则x0 称为函数f(x)的零点.

定理3（零点定理）设函数f(x)在闭区间[a, b]上连续, 且f(a)与f(b)异号, 那么在开区间(a, b)内至少有一点x 使f(x)=0.

定理4（介值定理）设函数f(x)在闭区间[a, b]上连续, 且f(a)¹f(b), 那么, 对于f(a)与f(b)之间的任意一个数C, 在开区间(a, b)内至少有一点x , 使得

f(x)=C .

推论  在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值.

    例  证明方程x 3-4x 2+1=0在区间（0, 1）内至少有一个根.

    证明： 函数f(x)= x 3-4x 2+1在闭区间[0, 1]上连续, 又f(0)=1>0,  f(1)=-2<0.

根据零点定理, 在(0, 1)内至少有一点x , 使得f(x)=0, 即  x 3-4x 2+1=0  (0<x<1).

这等式说明方程x 3-4x 2+1=0在区间（0, 1）内至少有一个根是x .

例 设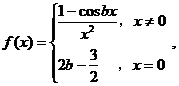确定值使得在处连续.

解  ，

，解b=1或b=3为所求.

例 证明方程在区间内至少有一个根.

证明 设，因为是初等函数，所以在闭区间上连续，又,由零点定理知至少有一个点使得，就是方程的根.

例 设函数在闭区间上连续，且，证明在开区间内至少有一点x，使.

证明 设，则，由于在闭区间上连续，所以在闭区间上连续，从而存在使得，即