理解导数的概念及其几何意义，了解函数的可导性与连续性之间的关系；了解导数作为函数变化率的实际意义；掌握导数的有理运算法则和复合函数的求导法，掌握基本初等函数的导数公式；理解微分的概念，了解微分概念中所包含的局部线性化思想，了解微分的有理运算法则和一阶微分形式不变性；了解高阶导数的概念，掌握初等函数一阶、二阶导数的求法；掌握利用一阶导数判断函数的单调性的方法；理解函数的极值概念，掌握利用导数求函数的极值的方法，会解简单一元函数的最大值与最小值的应用题；会用二阶导数判断函数图形的凹凸性及拐点，能描绘简单函数的图形.
导数的概念及其几何意义，函数的可导性与连续性之间的关系；导数的有理运算法则和复合函数的求导法，基本初等函数的导数公式；微分的概念，微分的有理运算法则和一阶微分形式不变性；高阶导数的概念及求法；利用一阶导数判断函数的单调性；函数的极值概念，利用导数求函数的极值，用二阶导数判断函数图形的凹凸性及拐点，描绘简单函数的图形.
第十九讲 导数问题引例
1.变速直线运动的瞬时速度问题：
设在直线上运动的一质点的位置方程为
（
表示时刻），又设当
为
时刻时，位置在
处，问：质点在
时刻的瞬时速度是多少？
为此，可取
近邻的时刻
，
，也可取
，在由
到
这一段时间内，质点的平均速度为
,显然当
与
越近，用
代替
的瞬时速度的效果越佳，特别地，当
时，
某常值
，那么
必为
点的瞬时速度，此时，
.
2.平面曲线的切线斜率问题：
切线的概念在中学已见过.从几何上看，在某点的切线就是一直线，它在该点和曲线相切.准确地说，曲线在其上某点M的切线是割线
当
沿该曲线无限地接近于
点的极限位置.
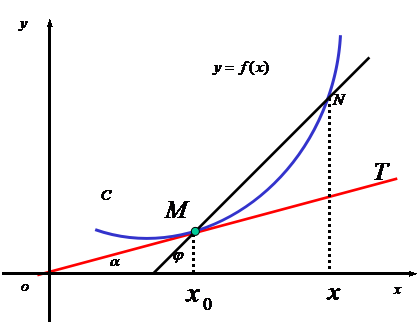
设曲线方程为
，设
点的坐标为
，动点
的坐标为
，要求出曲线在
点的切线，只须求出
点切线的斜率
.由上知，
恰好为割线
的斜率的极限.我们不难求得
的斜率为：
；因此，当
时，其极限存在的话，其值就是
，即
.
若设
为切线的倾角，则有
.