第三十一讲 微分的定义

微分的定义

先观察一个具体的问题，设一边长为x的正方形，它的面积为A＝是的函数，若边长增加，相应地正方形的面积得到增量：.它是有两部分组成，第一部分是的线性函数，第二部分，由此可见，当很小时，影响正方形面积增量的主要是：，而可忽略不计，因而用近似代替，其误差，即以为边的小正方形的面积.其中，是不依赖于的常数，且 ，我们称为函数A＝在点处相应于自变量的增量的微分.

定义 若函数在点处具有导数，则称为函数在点处相应于自变量的增量的微分，记作  ，此时也称函数在点是可微函数.在任意点处的微分，称为函数的微分，记作.

结论 函数 在任意点处的可微的充分必要条件是函数在点处的可导.

例1求在处的微分，并求此时的微分.

      解（1）

（2）

例2求的微分.

    解 

注：（1）上例说明自变量的增量就是函数的微分，通常称为自变量的微分，记为.从此，的微分又可记为          ……….（1）

（2）说明函数的微分等于函数的导数与自变量微分的乘积.若在（1）式两边同时除以，得                                     ……... 

（3）说明函数的导数等于函数的微分与自变量微分之商.因此，导数亦称微商.此记号就可看成是分子为，分母为的分式.

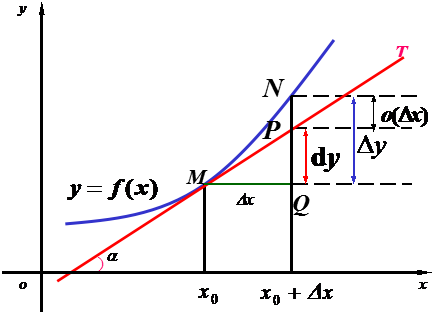
微分的几何意义

如图，函数的图形是一条曲线，直线是曲线在点处的切线，其倾角为，则其斜率为，当自变量由增加+到时，函数相应的增量为

，

又在M（）点，函数的切线的斜率为， 

从而得：PQ= MQ  =是曲线上的点的纵坐标的增量.是曲线在M点的切线上的点的纵坐标的增量.

当时，故常用来代替，用于近似的计算: