第三十三讲 函数单调性的判定法

 

第一章第一节中已经对函数的单调性作过描述，下面看看函数的单调性是否与导函数的符号有关呢?为此，我们进一步地作图，希望从中获得更多的感性认识.

 

 

 

 

 

 

 

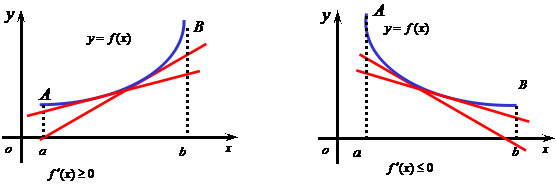
函数在上单调增加(减少)，则它的图形是一条沿轴正向上升(下降)的曲线， 曲线上各点处的切线之斜率均为正的(负的)，即：

  ()

这表明：函数的单调性确实与其导数的符号有关，因此，可以利用导数的符号来判定函数的单调性.

定理：设函数在[a,b]上连续，在内可导.

（1）如果在内，那末函数在[a,b] 上单调增加；

（2）如果在内，那末函数在[a,b] 上单调减少.

例1  判定函数在[0，2]上的单调性.

解  因为在（0，2）内

所以由判定法可知，函数在[0，2]上单调增加.

例2  讨论函数.

解  

函数的定义域为（－∞，+∞），因为在（－∞，0）内，所以函数在（－∞，0）上单调减少；因为在（0，+∞）内，所以函数在[0，+∞]上单调增加.

注意:

①函数的单调性是一个区间上的性质，要用导数在这一区间上的符号来判定，而不能用一点处的导数符号来判别一个区间上的单调性．

②定理中的区间换成其它有限或无限区间，结论仍然成立.

单调区间求法

问题: 如上例，函数在定义区间上不是单调的，但在各个部分区间上单调．

定义 若函数在其定义域的某个区间内是单调的，则该区间称为函数的单调区间.

导数等于零的点和不可导点，可能是单调区间的分界点．

例3  确定函数的单调区间.

解  这函数的定义域为（－∞，＋∞），求这函数的导数：

，

解方程，即解

得出它在函数定义域（－∞，＋∞）内的两个根、.这两个根把（－∞，＋∞）分成三个部分区间，[1,2]及.

在区间（－∞，1）内，，，所以，因此，函数在内单调增加.在区间（1，2）内，、，所以，因此，函数在[1，2]上单调减少.在区间（2，+∞）内，、，所以，因此，函数在上单调增加.

例4  讨论函数的单调性.

解  这函数的定义域为（－∞，＋∞）.

函数的导数.显然，除了点使，在其余各点处均有.因此函数在区间及上都是单调增加的，从而在整个定义域（―∞，＋∞）内是单调增加的，在处曲线有一水平切线.

注意：区间内个别点导数为零,不影响区间的单调性.

例5  证明：当时，.

证明  令，则

在上连续，在（1，+∞）内，因此在上单调增加，从而当时，.

由于，故，即

亦即          .

例6  试证明：当时， 有 .

解:作辅助函数 ，

，

，

当时，   ，  ，

故  ，

在上单调增加，从而有 ，

而 ，

于是 ，在上也单调增加.

从而有 ，

即      .