第三十五讲 函数极值的判定法
1、极值的定义
设函数![]() 在区间
在区间![]() 内有定义,点
内有定义,点![]() 是
是![]() 内的一点.若存在点
内的一点.若存在点![]() 的一个邻域,对于该邻域内任何异于
的一个邻域,对于该邻域内任何异于![]() 的点
的点![]() ,不等式
,不等式
![]() (
(![]() )
)
成立,称![]() 是函数
是函数![]() 的一个极大值(极小值);称点
的一个极大值(极小值);称点![]() 是函数
是函数![]() 的极大值点(极小值点).
的极大值点(极小值点).
函数的极大值与极小值统称为函数的极值;
使函数取得极值的点统称为极值点.
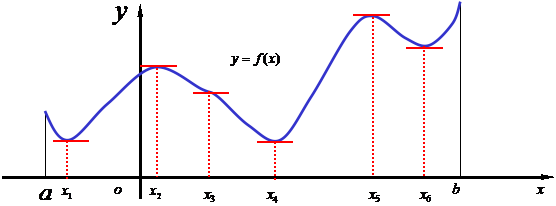
关于函数的极值,如下几点注记是十分重要的.
①函数的极值概念是一个局部概念.
如果![]() 是函数
是函数![]() 的一个极大值,那只是对
的一个极大值,那只是对![]() 的一个局部范围来说
的一个局部范围来说![]() 是
是![]() 的一个最大值.但对于整个函数的定义域来说,
的一个最大值.但对于整个函数的定义域来说,![]() 就不一定是最大值了.对于极小值也是类似的.
就不一定是最大值了.对于极小值也是类似的.
②极小值有可能较极大值更大.
如图: ![]() (
( ![]() 是极大值, 而
是极大值, 而![]() 是极小值 )
是极小值 )
2、函数极值的求法
函数极值存在的必要条件
定理1 设函数![]() 在点
在点![]() 处可导,且在
处可导,且在![]() 处取得极值,那末这函数在
处取得极值,那末这函数在![]() 处的导数为零,即
处的导数为零,即![]() .
.
证 为确定起见,假定![]() 是极大值(极小值的情形可类似地证明).根据极大值的定义,在
是极大值(极小值的情形可类似地证明).根据极大值的定义,在![]() 的某个去心邻域内,对于任何点x,
的某个去心邻域内,对于任何点x,![]() 均成立.于是,
均成立.于是,
当![]() 时,
时,
![]()
因此 ![]() ;
;
当![]() 时
时
![]()
因此 ![]() ;
;
从而得到 ![]() .
.
定义:使导数为零的点(即方程![]() 的实根)叫做函数
的实根)叫做函数![]() 的驻点.
的驻点.
注意:
可导函数![]() 的极值点必定是它的驻点,但函数的驻点却不一定是极值点.例如
的极值点必定是它的驻点,但函数的驻点却不一定是极值点.例如![]() 的导数
的导数![]() ,
,![]() ,因此
,因此![]() 是这可导函数的驻点,但
是这可导函数的驻点,但![]() 却不是这函数的极值点.
却不是这函数的极值点.
函数极值存在的第一种充分条件
定理2 设函数![]() 在点
在点![]() 的一个邻域内可导且
的一个邻域内可导且![]() .
.
(a)如果当![]() 取
取![]() 左侧邻近的值时,
左侧邻近的值时,![]() 恒为正;当
恒为正;当![]() 取
取![]() 右侧邻近的值时,
右侧邻近的值时,![]() 恒为负,那末函数
恒为负,那末函数![]() 在
在![]() 处取得极大值;
处取得极大值;
(b)如果当![]() 取
取![]() 左侧邻近的值时,
左侧邻近的值时,![]() 恒为负;当
恒为负;当![]() 取
取![]() 右侧邻近的值时,
右侧邻近的值时,![]() 恒为正,那末函数
恒为正,那末函数![]() 在
在![]() 处取得极小值;
处取得极小值;
(c)如果当![]() 取
取![]() 左右两侧邻近的值时,
左右两侧邻近的值时,![]() 恒为正或恒为负,那末函数
恒为正或恒为负,那末函数![]() 在
在![]() 处没有极值.
处没有极值.
定理2也可简单地这样说:当![]() 在
在![]() 的邻近渐增地经过
的邻近渐增地经过![]() 时,如果
时,如果![]() 的符号由正变负,那末
的符号由正变负,那末![]() 在
在![]() 处取得极大值;如果
处取得极大值;如果![]() 的符号由负变正,那末
的符号由负变正,那末![]() 在
在![]() 处取得极小值;如果
处取得极小值;如果![]() 的符号并不改变,那末
的符号并不改变,那末![]() 在
在![]() 处没有极值.
处没有极值.
求极值的步骤:
(1)求导数![]() ;
;
(2)求驻点,即求方程![]() 的根;
的根;
(3)考察![]() 在每个驻点的左、右的的正负号,判断极值点.
在每个驻点的左、右的的正负号,判断极值点.
例1求函数![]() 的极值.
的极值.
解 (1)![]() ,
,
(2)令![]() ,求得驻点
,求得驻点![]() ,
,![]() ;
;
(3)由![]() 来确定
来确定![]() 的符号:
的符号:
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ;
;
因而,函数![]() 在
在![]() 处取得极大值,在
处取得极大值,在![]() 处取得极小值.
处取得极小值.
(4)算出极大值![]() ,极小值
,极小值![]() .
.
函数求极值的第二种充分条件
定理3 设函数![]() 在
在![]() 处具有二阶导数且
处具有二阶导数且![]() ,
,![]() ,那末
,那末
(1)当![]() 时,函数
时,函数![]() 在
在![]() 处取得极大值;
处取得极大值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 处取得极小值.
处取得极小值.
证 在情形(1),由于![]() ,按二阶导数的定义有
,按二阶导数的定义有
![]()
根据函数极限的局部保号性,当![]() 在
在![]() 的足够小的去心邻域内时,
的足够小的去心邻域内时,
![]()
但,![]() ,所以上式即
,所以上式即
![]()
从而知道,对于这去心邻域内的x来说,![]() 与
与![]() 符号相反.因此,当
符号相反.因此,当![]() 即
即![]() 时,
时,![]() ;当
;当![]() 即
即![]() 时,
时,![]() .于是根据定理2知道,
.于是根据定理2知道,![]() 在点
在点![]() 处取得极大值.
处取得极大值.
类似地可以证明情形(2).
定理3表明,如果函数![]() 在驻点
在驻点![]() 处的二阶导数
处的二阶导数![]() ,那末该驻点
,那末该驻点![]() 一定是极值点,并且可以按二阶导数
一定是极值点,并且可以按二阶导数![]() 的符号来判定
的符号来判定![]() 是极大值还是极小值.
是极大值还是极小值.
注意:若![]() ,
,![]() 在
在![]() 处不一定取极值,仍用定理2判别.
处不一定取极值,仍用定理2判别.
例2 求函数![]() 的极值.
的极值.
解(1)![]() ,
,
(2)令![]() ,求得驻点
,求得驻点![]() ,
,![]() ,
,![]() ,
,
(3)![]() ,
,
(4)因![]() ,
,![]() 在
在![]() 处取得极小值,极小值为
处取得极小值,极小值为![]() .
.
(5)因![]() ,用定理3无法判别.考察一阶导数
,用定理3无法判别.考察一阶导数![]() 在驻点
在驻点![]() 及
及![]() 左右邻近的符号,
左右邻近的符号,
当![]() 以-1左侧邻近的值时,
以-1左侧邻近的值时,![]() ;当
;当![]() 以-1右侧邻近的值时,
以-1右侧邻近的值时,![]() ;因为
;因为![]() 的符号没有改变,所以
的符号没有改变,所以![]() 在
在![]() 处没有极值.同理,
处没有极值.同理,![]() 在
在![]() 处也没有极值.
处也没有极值.
注意:函数的不可导点,也可能是函数的极值点.
例3 函数![]() ,如图
,如图
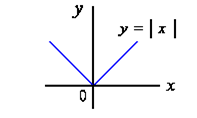
在![]() 处不可导,但函数在
处不可导,但函数在![]() 处取得极小值.点
处取得极小值.点![]() 是函数的极小值.
是函数的极小值.
例4 求函数![]() 的极值.
的极值.
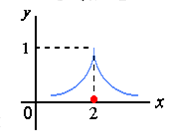
解 当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() 不存在.当
不存在.当![]() 时,即在(-∞,2)和(2,+∞)内的各点处,
时,即在(-∞,2)和(2,+∞)内的各点处,![]() 都存在,且
都存在,且![]() .根据定理1,
.根据定理1,![]() 在这两个区间内没有极值点,事实上,在(-∞,2)内,
在这两个区间内没有极值点,事实上,在(-∞,2)内,![]() ,函数
,函数![]() 单调增加;在(2,+∞)内,
单调增加;在(2,+∞)内,![]() ,函数单调减少.
,函数单调减少.
当![]() 时,
时,![]() 不存在,但函数
不存在,但函数![]() 在该点连续,再由上面得到的函数的单调性,可知
在该点连续,再由上面得到的函数的单调性,可知![]() 是函数
是函数![]() 的极大值.
的极大值.
这两例所反映的事实说明:函数的不可导点,也是函数可能的极值点,在讨论函数的极值时,应予以考虑.