第三十七讲 导数应用典型例题

例1 求下列函数的单调区间

（1）；（2）.

分析 此两题可归结为判断导数的符号，导数取正、取负的区间分别是函数的单调递增和单调递减区间.

解 （1），

，，

因此，函数当时单调递增；函数当时单调递减. 

（2）定义域与同号，得

.

因此，函数当时单调递增；函数当时单调递减. 

例2 求的单调区间.

解 ，解得驻点，

当时，当时，.

故函数单调递减区间为；故函数单调递增区间.

例3 设在区间二阶可导，且求证：在区间上严格单调递减. 

分析 要证在区间上严格单调递减，只要证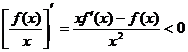 ，令，由条件它区间上连续，故只需证在区间上.

证明 令，求导得

故对，，

从而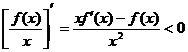，即在区间上严格单调递减. 

例4 证明 当时，.

证明 设，，

则，，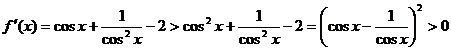

所以当时是单调增加，因此，（）

即（）.

例5求下列函数的极值：

（1）；     （2）；

（3）； （4）.

分析　首先对函数求导，求出驻点和一阶导数不存在点，然后用判断极值的第一充分条件和判断极值的第二充分条件，判断这些点是否是极值点，进而求出极值.

解（1），没有不可导的点.驻点为.由于在附近的符号左负右正，故为极小值；由于在附近的符号左正右负，故为极大值.

（2），不可导的点，由于在附近的符号左正右负，故为极大值.

（3）

令，则在内，驻点.由于，因而是极小值.

（4），则驻点为，

又，因此是极小值.

例6 问为何值时，点为曲线的拐点？

解 .

因为点为曲线的拐点，必有

得方程组

 解得，此时点为曲线的拐点.

例7　求函数的单调区间、极值、凹凸区间和曲线的拐点.

解　函数在区间内有定义.

.

令，解得，令.解得.

(1)当时，，因此当时，为单调增加.

当时，，因此当时，为单调减少.

当时，，因此当时，为单调减少.

当时，，因此当时，为单调减少.

当时，，因此当时，为单调增加.

(2) 极小值为，极大值为.

(3) 当时，，函数为上凸；

当时，，函数为下凸；

当时，，函数为上凸；

当时，，函数为下凸.

（4）拐点.