第二十二讲 导数的几何意义

由前面的讨论知：函数在的导数就是该曲线在点处的切线斜率，即，或为切线的倾角.从而，得切线方程为.

若，或  切线方程为：.

过切点，且与点切线垂直的直线称为在点的法线.如果，法线的斜率为，此时，法线的方程为：.

    如果=0，法线方程为.

例 求曲线在点处的切线与法线方程.

解  由于，所以在处的切线方程为：

                         ，

    当时，法线方程为：  

当时，法线方程为：  .

例 求曲线在它与直线的交点处的切线方程和法线方程.

解 解方程组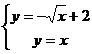求得交点为.

曲线在处的切线斜率为

，

所以切线方程为，即.

法线方程为，即.