第二十三讲 函数的可导性与连续性之间的关系
定理2 如果函数![]() 在
在![]() 点可导,那么在该点必连续.
点可导,那么在该点必连续.
注 1:本定理的逆定理不成立,即连续未必可导.
反例:![]() 在
在![]() 点连续,但不可导.
点连续,但不可导.
例1 求常数![]() 使得
使得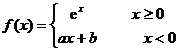 在
在![]() 点可导.
点可导.
解 若使![]() 在
在![]() 点可导,必使之连续,故
点可导,必使之连续,故![]()
![]() .
.
又若使![]() 在
在![]() 点可导,必使之左右导数存在,且相等,由函数知,左右导数是存在的,且
点可导,必使之左右导数存在,且相等,由函数知,左右导数是存在的,且
![]() ,
,
![]() ,
,
所以若有![]() ,则
,则![]() ,此时
,此时![]() 在
在![]() 点可导,所以所求常数为
点可导,所以所求常数为
![]() .
.
例2 设![]() 存在,求极限
存在,求极限![]() .
.
解 ![]()
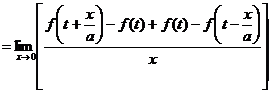
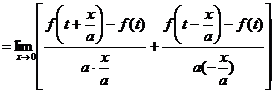
![]() .
.
例3 设函数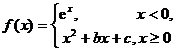 在
在![]() 处可导,求常数
处可导,求常数![]() 的值.
的值.
解 要求出两个常数![]() 的值,应建立关于
的值,应建立关于![]() 的两个方程,由可导必连续知,
的两个方程,由可导必连续知,![]() 在
在![]() 点可导,必有
点可导,必有![]() 在
在![]() 点连续,于是有
点连续,于是有
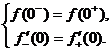
又因为![]()
![]() 所以
所以 ![]()
又![]()
![]()
所以![]() ,因此若函数
,因此若函数![]() 在
在![]() 处可导,则有
处可导,则有![]() ,
,![]()
例4 确定函数![]() 在
在![]() 处的连续性与可导性.
处的连续性与可导性.
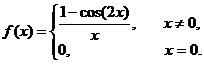
解 ![]()
![]()
由此可知,![]() 在
在![]() 处连续且可导.
处连续且可导.
例5 设函数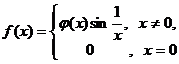 且
且![]() 求
求![]()
分析 分段函数在分段点的导数应当用定义计算,由于在![]() 点两侧的表达式相同,因此不需要分别求导.
点两侧的表达式相同,因此不需要分别求导.
解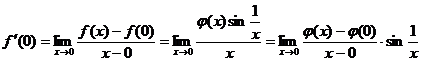
因为![]() ,
,![]() 所以
所以![]()
例6 证明双曲线![]() 上任一点处的切线与两坐标轴所围成图形的面积都等于
上任一点处的切线与两坐标轴所围成图形的面积都等于![]() ;
;
分析 利用导数的几何意义
证明 在双曲线![]() 上任取一点
上任取一点![]() ,则
,则![]() .由
.由![]() 得
得![]() 双曲线在点
双曲线在点![]() 处切线的斜率为
处切线的斜率为![]() 切线方程为
切线方程为
![]()
下面求切线在两个坐标轴上的截距.在切线方程中,令![]() 解得
解得![]() 令
令![]() 解得
解得![]() 故切线与两坐标轴所围成图形的面积为
故切线与两坐标轴所围成图形的面积为![]() .
.