第二十四讲 函数的和、差、积、商的求导法则
定理 1若函数![]() 和
和![]() 在点
在点![]() 都可导,则
都可导,则![]() 在
在![]() 点也可导,且
点也可导,且
![]() .
.
证明 ![]()
=![]() =
=![]()
所以![]() .
.
注 1:本定理可推广到有限个可导函数上去.
2:本定理的结论也常简记为![]() .
.
定理2若![]() 和
和![]() 在
在![]() 点可导,则
点可导,则![]() 在
在![]() 点可导,且有
点可导,且有![]() .
.
证明 ![]()
=![]()
=![]()
=![]()
=![]()
即 ![]() .
.
注 1:若取![]() 为常数,则有:
为常数,则有:![]() ;
;
2:本定理可推广到有限个可导函数的乘积上去,例如:
![]()
定理3 若![]() 都在
都在![]() 点可导,且
点可导,且![]() ,则
,则![]() 在
在![]() 点也可导,且
点也可导,且![]() .
.
证明 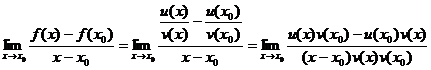
=![]()
=![]()
=![]()
即![]() .
.
注 1:本定理也可通过![]() ,及
,及![]() 的求导公式来得;
的求导公式来得;
2:本公式简化为![]() ;
;
3:以上定理1~3中的![]() ,若视为任意,并用
,若视为任意,并用![]() 代替,得函数的和、差、积、商的求导函数公式.
代替,得函数的和、差、积、商的求导函数公式.
例1设![]() ,求
,求![]() .
.
解 ![]()
![]()
![]()
![]() .
.
反函数的导数
定理1设![]() 为
为![]() 的反函数,若
的反函数,若![]() 在
在![]() 的某邻域内连续,严格单调,且
的某邻域内连续,严格单调,且![]() ,则
,则![]() 在
在![]() (即
(即![]() 点有导数),且
点有导数),且![]() .
.
证明 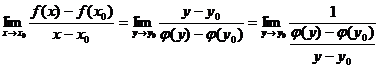
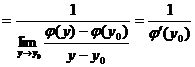
所以 ![]() .
.
注1:![]() ,因为
,因为![]() 在
在![]() 点附近连续,严格单调;
点附近连续,严格单调;
2:若视![]() 为任意,并用
为任意,并用![]() 代替,使得
代替,使得![]() 或
或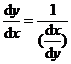 ,其中
,其中![]() 均为整体记号,各代表不同的意义;
均为整体记号,各代表不同的意义;
3:![]() 和
和![]() 的“′”均表示求导,但意义不同;
的“′”均表示求导,但意义不同;
4:定理1即说:反函数的导数等于直接函数导数的倒数;
5:注意区别反函数的导数与商的导数公式.
例1求![]() 的导数,
的导数,
解 由于![]() ,是
,是![]() 的反函数,由定理1得:
的反函数,由定理1得:
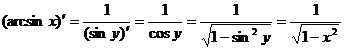 .
.
注:同理可证:![]() ;
;