第二十六讲 复合函数的求导公式
复合函数的求导问题是最最常见的问题,对一复合函数往往有这二个问题:1.是否可导?2.即使可导,导数如何求?复合函数的求导公式解决的就是这个问题.
定理(复合函数求导法则) 如果![]() 在
在![]() 点可导,且
点可导,且![]() 在
在![]() 点也可导,那么,复合函数
点也可导,那么,复合函数![]() 在
在![]() 点可导,且
点可导,且![]() ,或
,或![]() .
.
证明 ![]()
=![]() =
=![]()
注 1:若视![]() 为任意,并用
为任意,并用![]() 代替,便得导函数:
代替,便得导函数:
![]() ,或
,或![]()
或![]() .
.
2:![]() 与
与![]() 不同,前者是对变量
不同,前者是对变量![]() 求导,后者是对变量
求导,后者是对变量![]() 求导,注意区别.
求导,注意区别.
3:注意区别复合函数的求导与函数乘积的求导.
4:复合函数求导可推广到有限个函数复合的复合函数上去,如:
![]() 等.
等.
例1求![]() 的导数.
的导数.
解 ![]() 可看成
可看成![]() 与
与![]() 复合而成,
复合而成,
![]() ,
,![]() ,
,
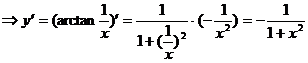 .
.
例2求![]() (
(![]() 为常数)的导数.
为常数)的导数.
解 ![]() 是
是![]() ,
,![]() 复合而成的.
复合而成的.
所以![]() .
.
由此可见,初等函数的求导数必须熟悉(i)基本初等函数的求导;(ii)复合函数的分解;(iii)复合函数的求导公式;只有这样才能做到准确.在解题时,若对复合函数的分解非常熟悉,可不必写出中间变量,而直接写出结果.
例3 ![]() ,求
,求![]() .
.
解 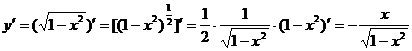 .
.
例4 ![]() ,求
,求![]()
解 ![]()
![]() .
.
例5 ![]() ,求
,求![]() .
.
解 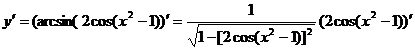
=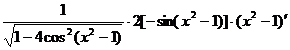
=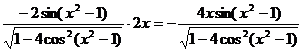 .
.
例6 ![]() ,求
,求![]() .
.
解 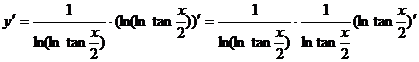
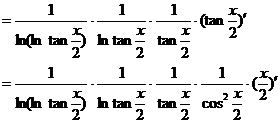
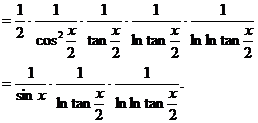 .
.
例7 ![]() ,求
,求![]() .
.
解 ![]()
![]()
![]() .
.