第四十一讲  不定积分的直接积分法

利用基本积分公式和不定积分的性质，可以直接计算一些较为简单的不定积分，这种方法一般称之为直接积分法.

                        典 型 例 题

例1  求.

解  由不定积分的性质和基本公式得

=

=

=

,和均为任意常数,则它们的代数和仍为任意常数，因此,令，故

.

例2  求下列不定积分：

（1）,          （2）.

解  （1）

.

（2）.

例3 求下列不定积分

（1）； （2）. 

分析 利用不定积分性质及基本积分公式求不定积分，若被积函数不是积分表中的类型，可先把被积函数进行恒等变形，然后利用积分性质化为若干个基本积分公式形式从而求得积分.

解（1）.

（2）

.

例4 求下列不定积分

（1）；（2）.

解（1）=

.

（2）=

=.

例5 求下列不定积分

（1）；   （2）. 

解（1）.

（2）=

.

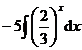
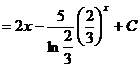
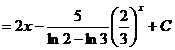例6 求下列不定积分

（1）；  （2）.

解（1）.

（2）.

例7 求下列不定积分

 （1）；（2）.

解（1）

.

（2）

例8 求下列不定积分

（1）；（2）.

解（1）.

.

（2）.

例9 求下列不定积分

（1）；       （2）；

（3）.

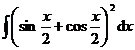解.（1）

.

（2）=

=

.

（3）

.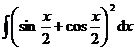