第四十五讲 换元积分法典型例题
例1求下列不定积分:
(1)![]() ; (2)
; (2)![]() .
.
分析 用凑微分法计算不定积分.
解(1)![]()
![]()
![]()
![]()
![]() .
.
(2)![]()
![]()
![]()
![]() .
.
例2求下列不定积分:
(1)![]() ;(2)
;(2)![]() .
.
解(1)![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
(2)![]()
![]()
![]() .
.
例3求下列不定积分:
(1)![]() ; (2)
; (2) ![]() .
.
解(1)![]()
![]() .
.
(2) ![]()
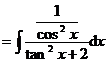
![]()
![]() .
.
例4 求下列不定积分:
(1) ![]() ;(2)
;(2)![]() .
.
解(1) ![]()
![]()
![]()
![]() .
.
(2)![]()
![]()
![]() .
.
例5求下列不定积分:
(1) ![]() ;(2)
;(2) 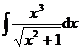 .
.
解 (1) ![]()
![]()
![]() .
.
(2) 
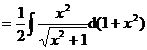
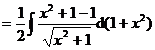
![]()
![]()
![]() .
.
例6 求不定积分![]() .
.
解![]()
![]()
![]()
![]()
![]() .
.
例7 求不定积分![]() .
.
解 ![]()
![]()
![]()
![]() .
.
例8求下列不定积分:
(1)![]() ;(2)
;(2)![]() ;
;
(3)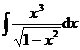 ;(4)
;(4) ![]() .
.
分析 用换元法计算不定积分.通过适当的积分变量的代换(令![]() 或
或![]() ),使得被积函数化简为
),使得被积函数化简为![]()
解(1)![]() ,则
,则![]() ,于是
,于是
![]()
![]()
![]()
![]()
![]() .
.
(2)令![]() ,则
,则![]() ,于是
,于是
![]()
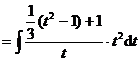
![]()
![]()
![]() .
.
(3)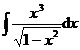
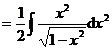
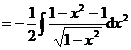
![]()
![]()
![]() .
.
(4) 令![]() ,则
,则![]() ,于是
,于是
![]()
![]()
![]()
![]()
![]()
![]()
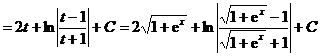 .
.