第五十九讲 定积分的两个简单应用

一、平面图形的面积

由定积分的几何意义，连续曲线与直线，，及轴所围成的曲边梯形的面积为.     

   若 在 上不都是非负的，则所围成的面积为

一般的，由上、下两条连续曲线，，及直线 ，，所围成的平面图形的面积为

.

二、闭区间上连续函数的平均值

在第一节中，由定积分中值定理，我们已经知道，连续函数在闭区间上的平均值为：.

典 型 例 题

例1求曲线和在上所围成的平面图形的面积.

解

   .

例2 求曲线和所围成的平面图形的面积.

解  

例3 求由直线和抛物线所围成的平面图形的面积.

解 ,

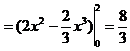
例4求由曲线和所围成的平面图形的面积.

解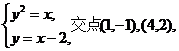 

   . 

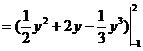
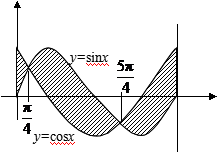
例5 求；x = 0以及

x =所围平面图形的面积（见右图）.

解 设所求面积为S，于是

根据三角函数的性质，有：

当或者时，

        ，

当时，，所以，

.

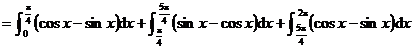
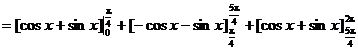
例6 求由曲线以及y = x2所围的平面图形的面积.

解 由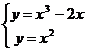得两曲线的交点

坐标是：

  (-1, 1)；(0, 0)；(2，4)

因此，所求平面图形的面积S为

由于在开区间(-1,0)范围内曲线

y = x3-2x在y = x2之上；在开区间

(0；2)范围内曲线在y = x2

之下.从而，所求面积S为：

.

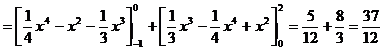例7 .

解  .