第四十九讲  定积分的定义

    定义  设函数在[a, b]上有界, 在[a, b]中任意插入若干个分点

a =x0< x1< x2<… < xn-1< xn=b, 

把区间[a, b]分成n个小区间:[x0, x1], [x1, x2], …, [xn-1, xn] , 称为子区间,各小段区间的长依次为x1=x1-x0, x2=x2-x1,…, xn =xn -xn-1.

在每个小区间[xi-1, xi]上任取一个点, 作函数值f (ξi)与小区间长度xi的乘积f (ξ i)xi (i=1, 2,× × ×, n) , 并作出和. 

记l = max{x1, x2,× × ×,xn}, 如果不论对[a, b]怎样分法, 也不论在小区间[xi-1, xi]上点ξi 怎样取法, 只要当l®0时, 上述和式的极限都存在, 则称函数f (x)在区间[a, b]上可积, 此极限值叫做函数f (x)在区间[a, b]上的定积分,记作, 即.

其中f (x)叫做被积函数, f (x)dx叫做被积表达式, x叫做积分变量, a 叫做积分下限, b 叫做积分上限, [a, b]叫做积分区间.

注意：定积分是研究分布在某区间上的非均匀量的求和问题，必须通过“分割、近似、求和、求极限”四个步骤完成，它表示了一个与积分变量无关的常量.

根据定积分的定义 

曲边梯形的面积为；

变速直线运动的路程为.

两点规定: 

        (1)当a=b时, . 

    (2)当时, .

.

    说明: 

    (1)定积分的值只与被积函数及积分区间有关, 而与积分变量的记法无关, 即

. 

(2)定积分的值与对区间[a, b]的分法及的取法无关.

定积分存在定理

(1) 如果f (x)在区间[a, b]上连续, 则f (x) 在[a, b]上可积.. 

（2）如果f (x)在区间[a, b]上有界，并且只有有限个第一类间断点，则f (x) 在[a, b]上可积.

被积函数在积分区间有界是可积的必要条件，在积分区间连续是可积的充分条件.

 定积分的几何意义

当f(x)³0时, 积分在几何上表示由曲线y=f (x)、两条直线x=a、x=b 与x轴所围成的曲边梯形的面积；当f(x)£0时, 由曲线y =f (x)、两条直线x=a、x=b 与x轴所围成的曲边梯形位于x轴的下方, 定义分在几何上表示上述曲边梯形面积的负值; 

.

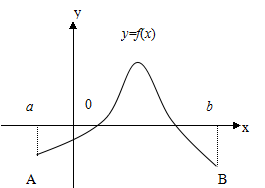当f (x)既取得正值又取得负值时, 

函数f(x)的图形某些部分在x轴的上方, 

而其它部分在x轴的下方. 

如果我们对面积赋以正负号, 

在x轴上方的图形面积赋以正号, 

在x轴下方的图形面积赋以负号, 则在一般情形下, 定积分的几何意义为：它是介于x轴、函数f(x)的图形及两条直线x=a、x=b之间的各部分面积的代数和.