第五十二讲 牛顿--莱布尼茨公式

应用定义去求定积分,尽管被积函数很简单,也是一件比较困难的事.所以,需要寻找简便而有效的计算方法,这就是牛顿—莱布尼兹公式.

    设物体从某定点开始作直线运动, 在t时刻所经过的路程为S(t), 速度为v=v(t)=(v(t)³0), 则在时间间隔[T1, T2]内物体所经过的路程S可表示为

        及,即. 

    上式表明, 速度函数v(t)在区间[T1, T2]上的定积分等于v(t)的原函数S(t)在区间[T1, T2]上的增量. 

这个特殊问题中得出的关系是否具有普遍意义呢.

一、 变上限的定积分

设函数在区间[a, b]上连续，对任意的x[a, b], 在区间[a, x]上也连续.所以函数在区间[a, b]上也可积.定积分的值依赖上限x，因此它也是定义在[a, b]上的函数，记作

                  ,

则叫做变上限的定积分.

定理1 若函数在区间[a, b]上连续，则变上限的定积分

                           ,

在区间[a, b]上可导，并且它的导数等于被积函数，即

                    .

由定理可知，如果函数在区间[a, b]上连续，则变上限的定积分就是在区间[a, b]上的一个原函数，即连续函数的原函数一定存在.

例1 计算：.

解 = .

例2 已知F(x)=,求.

解  = = =.

例3 设y = ,求.

解 积分上限是的函数，所以变上限的定积分是的复合函数，由复合函数求导法则 

==.

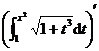二、 牛顿--莱布尼茨公式

    定理2  如果函数F (x) 区间[a, b]上连续，F (x)是f(x)在区间[a, b]上的一个原函数, 则

                     .

此公式称为牛顿--莱布尼茨公式, 也称为微积分基本公式.

    证明: 已知函数F(x) 是连续函数f(x) 的一个原函数, 又根据定理1, 积分上限函数

F(x)=也是f(x)的一个原函数. 于是有一常数C, 使F(x)-F(x)=C (a£x£b). 

当x=a时, 有F(a)-F(a)=C, 而F(a)=0, 所以C=F(a); 当x=b 时, 

F(b)-F(b)=F(a), 

所以F(b)=F(b)-F(a), 即. 

为了方便起见, 可把F(b)-F(a)记成, 于是

. 

牛顿—莱布尼兹公式揭示了定积分与原函数的关系，提供了解决定积分的一般方法.要求解定积分，首先要找到被积函数的原函数，而求原函数是不定积分的内容，由此，大家也可以进一步体会上一章内容的重要性.进一步揭示了定积分与被积函数的原函数或不定积分之间的联系.

例1 计算. 

解 . 

例2 计算下列定积分:

(1)，  (2) ，  (3) ，  (4) ，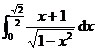

(5) .

解:(1) ，

(2) ===，

(3)==，

(4) =+

                 =+

                 =+=,

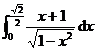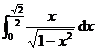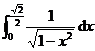
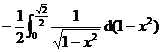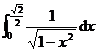
(5)=

=

                 =-=.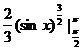