第六十三讲  一阶齐次微分方程

1、若一阶方程中的可写成的函数，即，则称方程为一阶齐次微分方程.

如可化为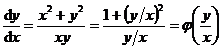，为齐次方程.

2、齐次方程可化为可分离变量型方程

对齐次方程，做变换，方程变为，即 ，两边积分后即得通解.

典型例题

例1 解方程.

解 将方程变形为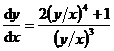，此题为齐次方程.

令，则，，

，，，

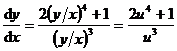，故通解为.

例2 解方程.

解 将方程变形为 此题为齐次方程.

令，则，

故 ，

因此，

得 ，

，，

故通解为.

例3 求下列微分方程的解：

（1）；

（2）.

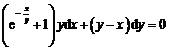解 （1）原方程可变形为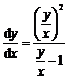，是齐次方程.

令，则，

代入原方程，得，

整理得，分离变量、积分且将代入得

                ，

即，C为任意常数.

（2）分析：方程中出现，考虑将看作函数，y看作自变量，

原方程可变形为，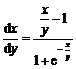

令，则，

代入原方程，得     ，

整理得   ，

分离变量、积分且将代入得

，C为任意常数.

例4 解方程.

解 将方程变形为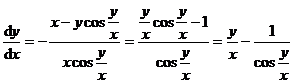，此题为齐次方程.

令，则，代入上式得 ，

从而有 ，，.

例5  解方程.

解 原方程可改写为,.

令，则有：，

有，，

原方程通解为.

例6 设有方程

                ，

试问为怎样的函数才能使给定的方程有通解？

分析 这是一个求解微分方程的相反问题，所给微分方程是齐次方程.

解 若令，则，

代入所给方程可得 

即 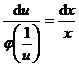，积分得.

由题设知原方程有通解，即，

所以，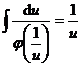

于是，，，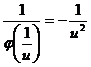

故.