第一章 函数与极限
　　　 第一节 函数
　　　 了解函数的概念、表示方法；函数的有界性、单调性、奇偶性、周期性；分段函数、复合函数的概念； 六种基本初等函数，初等函数的概念；简单实际问题函数关系的建立。
　　　 第二节 函数的极限
　　　 理解数列极限的概念、函数极限的概念；无穷小、无穷大概念及其相互关系；两个重要极限。
　　　 第三节 极限的运算
　　　 掌握极限的四则运算法则，复合函数的求极限法则，运用两个重要极限求极限的方法；无穷小的性质，用等价无穷小的性质求极限。
　　　 第四节 函数的连续性与间断点
　　　 掌握函数连续的概念，函数间断点的概念及分类；连续函数的四则运算法则，复合函数、反函数、初等函数的连续性；闭区间上连续函数的性质。

第二章 导数与微分
　　　 第一节 导数的概念
　　　 理解导数概念及其几何意义，掌握常见的基本初等函数的导数公式，明确函数的可导性与连续性的关系。
　　　 第二节 函数的和、差、积、商的求导法则
　　　 掌握函数的和、差、积、商的求导法则，能够用导数运算法则和初等函数的导数公式求正确求出函数的导数。
　　　 第三节 复合函数的求导法则
　　　 掌握复合函数的求导数方法，能够用复合函数的求导数方法求复合函数的导数。
　　　 第四节 高阶导数
　　　 理解高阶导数的定义，掌握求高阶导数的方法，能够求函数的高阶导数。
　　　 第五节 函数的微分
　　　 理解函数微分概念及其几何意义，掌握微分运算法则和基本初等函数的微分公式，掌握复合函数的微分法则和微分形式的不变性，能够正确求出函数的微分。
　　　 第六节 导数的几个简单应用
　　　 掌握利用求导数的方法判别函数的单调性，曲线的凹凸性，掌握求函数的极值的方法，了解简单函数图形的描绘方法。

第三章 不定积分
　　　 第一节 不定积分的概念与性质
　　　 理解原函数定义，理解不定积分的概念与性质及其几何意义，掌握不定积分的基本积分公式。
　　　 第二节 不定积分的直接积分法
　　　 掌握利用不定积分的基本公式、运算法则求不定积分的方法。
　　　 第三节 不定积分的换元积分法
　　　 重点掌握求不定积分的第一类换元积分法（凑微分法）、第二类换元积分法（去根号法）。
　　　 第四节 不定积分的分部积分法
　　　 重点能够用不定积分的分部积分法求函数的不定积分。

第四章 定积分
　　　 第一节 定积分的概念与性质
　　　 理解定积分的概念，定积分的性质及其几何意义，定积分的存在定理。
　　　 第二节 牛顿-莱布尼茨公式
　　　 重点掌握牛顿—莱布尼茨公式，能够用牛顿—莱布尼茨公式的方法求函数的定积分。
　　　 第三节 定积分的积分法
　　　 重点掌握用定积分的换元积分公式、定积分的分部积分公式，求函数的定积分的方法。
　　　 第四节 定积分的两个简单应用
　　　 掌握用定积分的方法求平面图形的面积的方法，掌握用定积分的方法求闭区间上连续函数的平均值的方法。

第五章 微分方程
　　　 第一节 微分方程的基本概念
　　　 明确微分方程的一些基本概念，主要包括：微分方程的阶，微分方程的解，微分方程的通解，微分方程的特解，微分方程的初始条件。
　　　 第二节 一阶微分方程
　　　 重点掌握解可分离变量的微分方程，一阶齐次微分方程，一阶线性微分方程的方法；记住相关的求微分方程解的公式。
　　　 第三节 二阶线性常系数齐次微分方程
　　　 明确二阶线性微分方程概念，二阶线性齐次微分方程解的结构，重点掌握解二阶线性常系数齐次线性微分方程的方法。
　　　 第四节 可降阶的高阶微分方程
　　　 掌握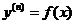型的阶微分方程的解法， 掌握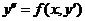型的二阶微分方程的解法， 掌握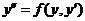型的二阶微分方程的解法。