|
|
4.代换的一致性及剪枝策略
(1)代换的一致性
定义:设代换集合Q={Q1,Q2,Q3…Qn}第i个代换Qi(i=1,2,…,n)为
Qi={ti1/xi2,ti2/xi2…,tim(i)/xim(i)}
tij为项,xij变元(j=1,2,m(i)),则代换集Q是一致的充要条件是如下两个元组
T={t11,t12,…,t1m(1),t21,…,t2m(2),…,tnm(n)}
X={x11,x12,…,x1m(1),x21,x2m(2),…,xnm(n)}可合一 |
例 1
Q1=f(g(x1))/x3,f(x2)/x4}={f(x2)/x3,f(x2)/x4}
Q2={x4/x3,g(x1)/x2}={f(x2)/x3,f(x2)/x4}
∴Q={Q1,Q2}是一致的
例 2
设Q1={a/x},Q2={b/x},则Q={Q1,Q2}是不一致的
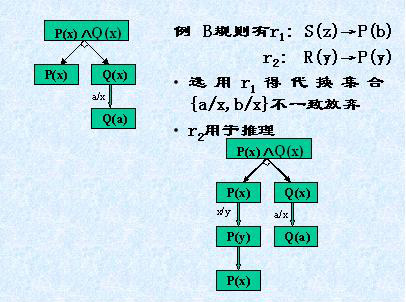
(2)剪枝策略
基本思想:每当选用一条规则时,就进行一次一致性检查,如果当前的部分解图是一致的,则继续向下扩展,否则放弃规则而选用其它候选规则。 |
  点击看大图 点击看大图 |
|
|
|