|
|
|
|
|
|
|
|
| |
|
|
|
|
|
| |
 |
|
|
| |
|
|
|
|
| |
|
点击看大图 |
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
点击看大图 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
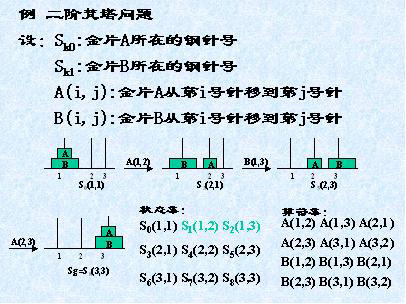
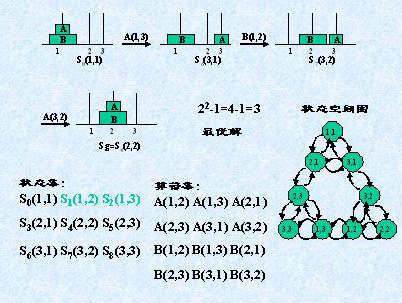
(5)解题过程
--*定义状态描述,定义一组算符
--*问题的求解过程是一个不断把算符作用于状态的过程
--*算符的一次使用,就使问题由一种状态转变为另一种状态,使用算符最少的解称为最优解
--*对任何一个状态,可使用的算符不止一个,生成的后继状态可能有多个,涉及搜索策略。
|
|
|
|
|
|
|
|
| 3
与/或树表示法:用于比较复杂的问题 |
(1)分解:问题分解为子问题,子问题分解为子问题。
例 P分解成P1,P2,P3三个子问题,只有当这三个子问题都可以解时,问题P才可解。P1,P2,P3之间存在“与”关系,节点P为与节点,用一条弧连接。
(2)等价变换:对于复杂的问题,还可利用同构或同态的等价变换,把它变换为若干个较容易求解的新问题。若新问题中有一个可求解,则原问题可解。
例 P被等价变换为三个新问题P1,P2,P3 ,任何一个Pi可解,P可解,则P1,P2,P3之间存在或关系,节点P称为或节点。
将上述两种方法结合使用,称为“与/或”树 |
|
|