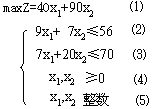§
2 分枝定界法 §
2 分枝定界法
|
分枝定界法是求解整数规划的常用算法,既可用来解全部变量取值都要求为整数的纯整数规划,又可用以求解混合整数规划。
 该算法的基本思路是:先不考虑整数限制,求出相应的线性规划的最优解,若此解不符合整数要求,则去掉不包含整数解的部分可行域,将可行域D分成 该算法的基本思路是:先不考虑整数限制,求出相应的线性规划的最优解,若此解不符合整数要求,则去掉不包含整数解的部分可行域,将可行域D分成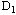 、 、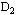 两部分(分枝)
,然后分别求解这两部分可行域对应的线性规划,如果它们的解仍不是整数解,则继续去掉不包含整数解的部分可行域,将可行域 两部分(分枝)
,然后分别求解这两部分可行域对应的线性规划,如果它们的解仍不是整数解,则继续去掉不包含整数解的部分可行域,将可行域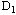 或 或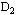 分成 分成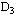 与 与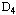 两部分,再求解 两部分,再求解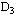 与 与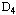 对应的线性规划,……,在计算中若已得到一个整数可行解 对应的线性规划,……,在计算中若已得到一个整数可行解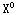 ,则以该解的目标函数值 ,则以该解的目标函数值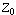 作为分枝的界限,如果某一线性规划的目标值Z≤ 作为分枝的界限,如果某一线性规划的目标值Z≤
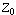 ,就没有必要继续分枝,因为分枝(增加约束)的结果所得的最优解只能比 ,就没有必要继续分枝,因为分枝(增加约束)的结果所得的最优解只能比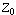 更差。反之若Z>
更差。反之若Z>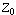 ,则该线性规划分枝后,有可能产生比
,则该线性规划分枝后,有可能产生比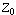 更好的整数解,一旦真的产生了一个更好的整数解,则以这个更好的整数解目标值作为新的界限,继续进行分枝,直至产生不出更好的整数解为止。
更好的整数解,一旦真的产生了一个更好的整数解,则以这个更好的整数解目标值作为新的界限,继续进行分枝,直至产生不出更好的整数解为止。
下面以实例来说明算法的步骤。
|
 例2
求解下面整数规划 例2
求解下面整数规划 |
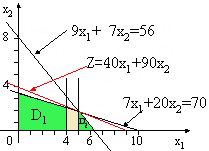
解:先不考虑条件⑸,求解相应的线性规划问题L,得最优解
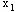 =4.81, =4.81,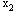 =1.82, =1.82,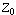 =356(见图) =356(见图)
|
该解不是整数解。选择其中一个非整数变量,如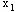 =4.81,对问题L分别增加约束条件: =4.81,对问题L分别增加约束条件:
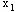 ≤4, ≤4,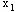 ≥5
将问题L分解为两个子问题 ≥5
将问题L分解为两个子问题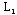 , , (分枝),也就是去掉问题L不含整数解的一部分可行域,将原可行域D变为 (分枝),也就是去掉问题L不含整数解的一部分可行域,将原可行域D变为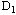 、 、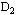 两部分(如图) 两部分(如图)
|
|
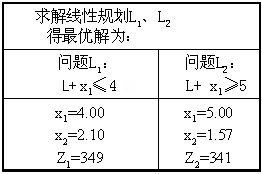
因为没有得到整数解,所以继续对L1进行分解,增加约束: 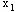 ≤2, ≤2,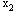 ≥3
将 ≥3
将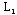 分解成问题 分解成问题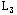 与 与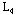 ,并求得最优解如下: ,并求得最优解如下:
|
问题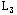 的解已是整数解,它的目标值 的解已是整数解,它的目标值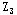 =340,大于问题L4的目标值,所以问题 =340,大于问题L4的目标值,所以问题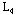 已无必要再分枝。但由于问题 已无必要再分枝。但由于问题 的目标值 的目标值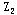 大于 大于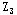 ,分解 ,分解 还有可能产生更好的整数解,因此继续对 还有可能产生更好的整数解,因此继续对 分枝。增加约束 分枝。增加约束
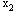 ≤1, ≤1,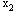 ≥2
将 ≥2
将 分解成问题 分解成问题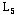 与 与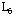 ,并求解,结果如下: ,并求解,结果如下:
|
问题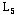 的 的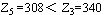 ,所以不必分解了;问题 ,所以不必分解了;问题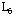 无可行解,于是可以断定问题 无可行解,于是可以断定问题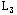 的解: 的解:
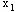 =4.00, =4.00,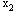 =2.00即为最优整数解。 =2.00即为最优整数解。
|
 整个分枝定界过程如下图所示: 整个分枝定界过程如下图所示: |
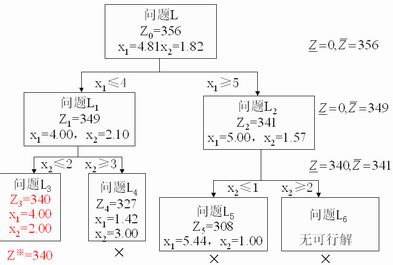
|
用分枝定界法求解整数规划的步骤可总结如下:
 步骤1:求解与整数规划相对应的线性规划L,若L无可行解,则整数规划也没有可行解,计算停;若L的最优解是整数解,则该解即为整数规划的最优解,计算停;若L的最优解不是整数解,则转步骤2。 步骤1:求解与整数规划相对应的线性规划L,若L无可行解,则整数规划也没有可行解,计算停;若L的最优解是整数解,则该解即为整数规划的最优解,计算停;若L的最优解不是整数解,则转步骤2。
 步骤2(分枝)在L的最优解中任选一个不符合整数条件的变量 步骤2(分枝)在L的最优解中任选一个不符合整数条件的变量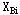 ,其值为 ,其值为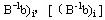 为小于 为小于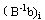 的最大整数,构造两个约束条件 的最大整数,构造两个约束条件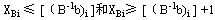
将这两个约束条件分别加在问题L的约束条件上,形成两个子问题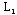 和 和 ,并求解 ,并求解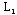 和 和 。
。
 步骤3(定界
)取整数解中最大目标值为界限值Z(下界),如果计算中尚无整数解,则取Z=-∞。检查分枝 步骤3(定界
)取整数解中最大目标值为界限值Z(下界),如果计算中尚无整数解,则取Z=-∞。检查分枝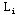 ,若它的最优解不是整数解,且 ,若它的最优解不是整数解,且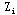 >Z,则重复步骤2,若 >Z,则重复步骤2,若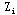 ≤Z,则 ≤Z,则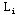 不再分枝。 不再分枝。
重复步骤2、步骤3,直至所有分枝都不能再分解为止,这时界限值Z对应的整数解即为原问题的最优解。
用分枝定界法可解纯整数规划问题和混合整数规划问题。它比穷举法优越,因为它仅在一部分可行的整数解中寻求最优解,计算量比穷举法小。若变量数目很大,其计算工作量也是相当可观的。
|