|
|||
 1.1
多阶段决策问题在研究社会经济、经营管理和工程技术领域内的有关问题中，有一类特殊形式的动态决策问题—多阶段决策问题。在多阶段决策过程中，系统的动态过程可以按照时间进程分为相互联系而又相互区别的各个阶段，在每个阶段都要进行决策。系统在每个阶段存在许多不同的状态，在某个时点的状态往往要依某种形式受到过去某些决策的影响，而系统的当前状态和决策又会影响系统过程今后的发展。因而在寻求多阶段决策问题的最优解时，重要的是不能仅仅从眼前的局部利益出发进行决策，而需要从系统所经过的整个期间的总效应出发，有预见性地进行动态决策，找到不同时点的最优决策及整个过程的最优策略。  下面举例说明什么是多阶段决策问题。 |
|||
 例1（最短路线问题）在线路网络图5—1中，从A至E有一批货物需要调运。图上所标数字为各节点之间的运输距离，为使总运费最少，必须找出一条由A至E总里程最短的路线。
|
|||
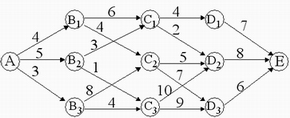
| 为了找到由A至E的最短线路，可以将该问题分成A—B—C—D—E
4个阶段，在每个阶段都需要作出决策，即在A点需决策下一步到B1还是到B2或B3；同样，若到达第二阶段某个状态，比如B1 ，需决定走向C1还是C2
；依次类推，可以看出：各个阶段的决策不同，由A至E的路线就不同，当从某个阶段的某个状态出发作出一个决策，则这个决策不仅影响到下一个阶段的距离，而且直接影响后面各阶段的行进线路。所以这类问题要求在各个阶段选择一个恰当的决策，使这些决策序列所决定的一条路线对应的总路程最短。 |
|||
| 例2（带回收的资源分配问题）某厂新购某种机床125台。据估计，这种设备5年后将被其它设备所代替。此机车如在高负荷状态下工作，年损坏率为1/2，年利润为10万元；如在低负荷状态下工作，年损坏率为1/5，年利润为6万元。问应如何安排这些机床的生产负荷，才能使5年内获得的利润最大？ |
|||
| 本问题具有时间上的次序性，在五年计划的每一年都要作出关于这些机床生产负荷的决策，并且一旦作出决策，不仅影响到本年利润的多少，而且影响到下一年初完好机床数，从而影响以后各年的利润。所以在每年初作决策时，必须将当年的利润和以后各年利润结合起来，统筹考虑。
与上面例1、例2类似的多阶段决策问题还有资源分配、生产存贮、可靠性、背包、设备更新问题等等。 |
|||
1.2
动态规划的基本概念 1.阶段动态规划问题通常都具有时间或空间上的次序性，因此求解这类问题时，首先要将问题按一定的次序划分成若干相互联系的阶段，以便能按一定次序去求解。如例1，可以按空间次序划分为A—B—C—D—E 4个阶段，而例2，按照时间次序可分成5个阶段。 2.状态在多阶段决策过程中，每阶段都需要作出决策，而决策是根据系统所处情况决定的。状态是描述系统情况所必需的信息。如例1中每阶段的出发点位置就是状态，例2中每年初拥有的完好机床数是作出机床负荷安排的根据，所以年初完好机床数是状态。一般地，状态可以用一个变量来描述，称为状态变量。记第k 阶段的状态变量为  ,k=1,2,
…,n.3.决策多阶段决策过程的发展是用各阶段的状态演变来描述的，阶段决策就是决策者从本阶段某状态出发对下一阶段状态所作出的选择。描述决策的变量称为决策变量，当第k 阶段的状态确定之后，可能作出的决策要受到这一状态的影响。这就是说决策变量  还是状态变量
的函数，因此，又可将第k阶段状态下的决策变量记为()。在实际问题中，决策变量的取值往往限制在某一范围之内，此范围称为允许决策变量集合，记作Dk( )。如例2中取高负荷运行的机床数为决策变量，则0≤≤（是k阶段初完好机床数）为允许决策变量集合。4.状态转移方程在多阶段决策过程中，如果给定了k 阶段的状态变量 和决策变量，则第k+1阶段的状态变量 也会随之而确定。也就是说是xk和函数，这种关系可记为
=T(xk,
) 称之为状态转移方程。 |
|||
| 5.策略 在一个多阶段决策过程中，如果各个阶段的决策变量 ()
（k=1，2，…，n）都已确定，则整个过程也就完全确定。称决策序列 为该过程的一个策略，从阶段k到阶段n的决策序列称为子策略，表示成 。如例1中，选取一路线
就是一个策略：
由于每一阶段都有若干个可能的状态和多种不同的决策，因而一个多阶段决策的实际问题存在许多策略可供选择，称其中能够满足预期目标的策略为最优策略。例1中存在12条不同路线，其中  是最短线路。6.指标函数用来衡量过程优劣的数量指标，称为指标函数。在阶段k的 状态下执行决策，不仅带来系统状态的转移，而且也必然对目标函数给予影响，阶段效应就是执行阶段决策时给目标函数的影响。 多阶段决策过程关于目标函数的总效应是各阶段的阶段效应累积形成的。常见的全过程目标函数有以下两种形式：（1）全过程的目标函数等于各阶段目标函数的和，即：
（2）全过程的目标函数等于各阶段目标函数的积，即： 指标函数的最优值，称为最优函数值。一般，  （x1）表示从第1阶段 状态出发至第n阶段（最后阶段）的最优指标函数，
 （）表示从第k阶段状态出发至第n阶段的最优指标函数(k=1，2，…，n）。 |
§
1 多阶段决策问题 
