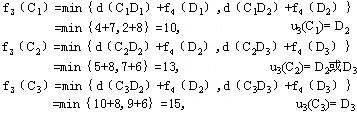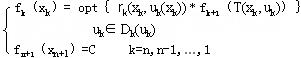|
||||||||
| 多阶段决策过程的特点是每个阶段都要进行决策，具有n个阶段的决策过程的策略是由n个相继进行的阶段决策构成的决策序列。由于前阶段的终止状态又是后一阶段的初始状态，因此确定阶段最优决策不能只从本阶段的效应出发，必须通盘考虑，整体规划。就是说，阶段k的最优决策不应只是本阶段的最优，而必须是本阶段及其所有后续阶段的总体最优，即关于整个后部子过程的最优决策。 对此，贝尔曼在深入研究的基础上，针对具有无后效性的多阶段决策过程的特点，提出了著名的多阶段决策的最优性原理： “整个过程的最优策略具有这样的性质：即无论过程过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。” 简而言之，最优性原理的含意就是：最优策略的任何一部分子策略也必须是最优的。 |
||||||||
如例1， 是由A到E的最短路线，我们在该路线上任取一点
，按照最优性原理 应该是到E的最短路。很容易用反证法证明这一结论的正确性，从而说明最优性原理的正确性。按最优性原理，可以将例1分成A—B—C—D—E 4个阶段，由后向前逐步求出各点到E的最短线路，直至求出A至E的最短线路。 例1的路线图  |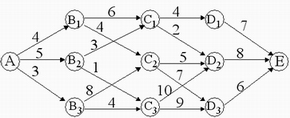
||||||||
 K=4时，出发点有D1，D2，D3，记
K=3时，出发点有C1，C2，C3
|
||||||||
为了找出最短线路，再按计算顺序反推回去，可求出最优决策序列，即由
组成最优策略，也就是最短线路为：
|
||||||||
从上面的例子不难看出，对于最短线路问题，有如下的递推关系（函数方程）：
|
||||||||
一般情况下，多阶段决策问题存在下面的递推关系：
|
||||||||
这里 ( ,
 )是第阶段采用决策产生的阶段效应； 是边界条件；“﹡”号大多数情况下是
“+”号，也可能是“×”号。称上述递推关系为动态规划的基本方程，这个方程是最优化原理的具体表达形式。 |
||||||||
在基本方程中， 都是已知函数，最优子策略 （）与 之间是递推关系，要求出（）及，需要先求出，这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。 |
||||||||
另一方面，由于k+1阶段的状态 =T(,
 )是由前面的状态和决策所形成的，在计算时还不能具体确定的，这就要求必须就k+1阶段的各个可能状态计算，因此动态规划不但能求出整个问题的最优策略和最优目标值，而且还能求出决策过程中所有可能状态的最优策略及最优目标值。 |
§
2 动态规划的基本概念和最优化原理 
