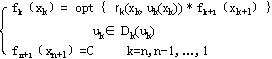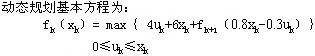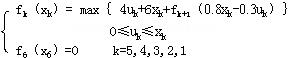§
3 建立动态规划数学模型的步骤 §
3 建立动态规划数学模型的步骤
|
“最优化原理”是动态规划的核心,所有动态规划问题的递推关系都是根据这个原理建立起来的,并且根据递推关系依次计算,最终可求得动态规划问题的解。
一般来说,利用动态规划求解实际问题需先建立问题的动态模型,具体步骤如下:
 ⒈将问题按时间或空间次序划分成若干阶段。有些问题不具有时空次序,也可以人为地引进时空次序,划分阶段。 ⒈将问题按时间或空间次序划分成若干阶段。有些问题不具有时空次序,也可以人为地引进时空次序,划分阶段。
 ⒉正确选择状态变量 ⒉正确选择状态变量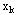 。这一步是形成动态模型的关键,状态变量是动态规划模型中最重要的参数。一般来说,状态变量应具有以下三个特性: 。这一步是形成动态模型的关键,状态变量是动态规划模型中最重要的参数。一般来说,状态变量应具有以下三个特性:
⑴要能够用来描述决策过程的演变特征。
⑵要满足无后效性。即如果某阶段状态已给定后,则以后过程的进展不受以前各状态的影响,也就是说,过去的历史只通过当前的状态去影响未来的发展。
⑶递推性。即由k阶段的状态变量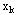 及决策变量uk可以计算出k+1阶段的状态变量 及决策变量uk可以计算出k+1阶段的状态变量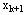 。 。
 ⒊确定决策变量 ⒊确定决策变量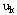 及允许决策变量集合Dk( 及允许决策变量集合Dk(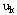 )。 )。
 ⒋根据状态变量之间的递推关系,写出状态转移方程: ⒋根据状态变量之间的递推关系,写出状态转移方程:
 ⒌建立指标函数。一般用 ⒌建立指标函数。一般用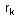 ( (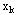 , ,
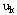 )描写阶段效应, )描写阶段效应,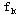 ( (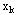 )表示k—n阶段的最优子策略函数。 )表示k—n阶段的最优子策略函数。
 ⒍建立动态规划基本方程: ⒍建立动态规划基本方程:
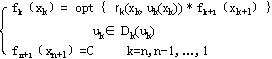
以上是建立动态规划模型的过程,这个过程是正确求解动态规划的基础。
在动态规划基本方程中, 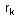 ( (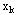 , ,
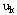 ), ),
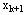 =T( =T(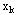 , ,
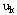 )都是已知函数,最优子策略 )都是已知函数,最优子策略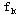 ( (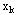 )与 )与
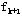 ( (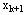 )之间是递推关系,要求出 )之间是递推关系,要求出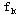 ( (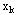 )及 )及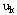 ( (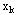 ),需要先求出 ),需要先求出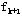 ( (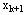 ),这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。由后向前逐步计算,最终可以算出全过程的最优策略函数值及最优策略。 ),这就决定了应用动态规划基本方程求最优策略总是逆着阶段的顺序进行的。由后向前逐步计算,最终可以算出全过程的最优策略函数值及最优策略。
|
另一方面,由于k+1阶段的状态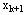 =T( =T(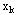 , ,
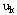 )是由前面的状态 )是由前面的状态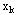 和决策 和决策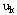 所形成的,在计算 所形成的,在计算
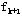 ( (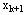 )时还不能具体确定 )时还不能具体确定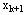 的值,所以,这就要求必须就k+1阶段的各个可能状态计算 的值,所以,这就要求必须就k+1阶段的各个可能状态计算
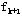 ( (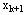 ),因此动态规划方法不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。 ),因此动态规划方法不但能求出整个问题的最优策略和最优目标值,而且还能求出决策过程中所有可能状态的最优策略及最优目标值。
|
下面就按上述步骤求解例2。
|
 例2(带回收的资源分配问题)某厂新购某种机床125台。据估计,这种设备5年后将被其它设备所代替。此机床如在高负荷状态下工作,年损坏率为1/2,年利润为10万元;如在低负荷状态下工作,年损坏率为1/5,年利润为6万元。问应如何安排这些机床的生产负荷,才能使5年内获得的利润最大? 例2(带回收的资源分配问题)某厂新购某种机床125台。据估计,这种设备5年后将被其它设备所代替。此机床如在高负荷状态下工作,年损坏率为1/2,年利润为10万元;如在低负荷状态下工作,年损坏率为1/5,年利润为6万元。问应如何安排这些机床的生产负荷,才能使5年内获得的利润最大?
|
解:以年为阶段,k=1,2,3,4,5, 取k年初完好的机床数为状态变量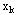 ,
以k年初投入高负荷运行的机床数为决策变量 ,
以k年初投入高负荷运行的机床数为决策变量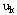 ,则低负荷运行机床数是 ,则低负荷运行机床数是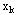 - -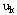 ,于是状态转移方程为: ,于是状态转移方程为:
以利润为目标函数,则k年利润为:
记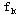 ( (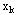 )为k年至5年末最大总利润,则动态规划基本方程为: )为k年至5年末最大总利润,则动态规划基本方程为:
|
以上是建立动态模型的过程,下面具体求解。
注意动态规划基本方程为:


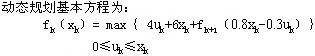

|
至此已算得最大总利润2790万元,再按与计算过程相反的顺序推回去,可得最优计划如下表所示:
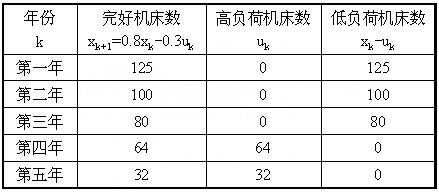 |