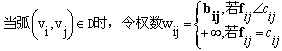|
||
| 在实际网络问题中,不仅要考虑从 最小费用最大流问题的一般提法:已知容量网络D=(V,A,C),每条弧(
|
||
| 从上一讲可知,最大流的求法就是在容量网络上从某个可行流出发,设法找到一条从 |
||
| 现在要寻求最小费用的最大流,我们首先考察一下,当沿着一条关于可行流 f 的增广链μ,以θ=1调整
f 得到新的可行流 f′时,总费用b(f′)比b(f )增加多少? ∵在前向弧μ+上 ∴ b(f′)-b(f )=[∑ 即沿着关于可行流 f 的增广链μ,增加一个单位运量时,所增加的总费用是μ上所有前向弧的费用之和减去所有后向弧的费用之和。 我们称此费用为该增广链μ的费用。 |
||
| 可以证明:若 f 是流量为v(f )的所有可行流中费用最小者,而μ是关于f 的所有增广链中费用最小的增广链,那么沿着μ去调整
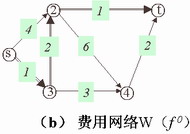
f , 得到的可行流f ′就是流量为v(f ′)的所有可行流中的最小费用流。这样,当 f ′是最大流时,它就是我们所要求的最小费用最大流。 上述命题为我们提供了寻找最小费用最大流的思路:先找一个最小费用可行流,再找出关于该可行流的最小费用增广链,沿此链调整流量,则得到一个新的流量增大了的最小费用流,然后对新的最小费用流重复上述方法,一直调整到网络的最大流出现为止,便得到了所考虑网络的最小费用最大流。 由于 为此,构造一个有向费用网络W( f ),它的顶点与原网络完全相同,而把原网络中的每一条弧(
|
||
| 上述定义式的含义是:在增广链的前向弧上,当 经上述处理后,在费用、容量网络中寻找关于 f 的最小费用增广链问题,就转化为在有向费用网络W( f )中寻找从 |
||
| 具体算法步骤如下: ⑴取0流为初始最小费用可行流 ⑵若在k-1步(k=1,2, …)得最小费用流 ⑶在网络W( ⑷在原网络图中与这条最短路相应的增广链上,对流量v( 调整后得新的最小费用流 |
||
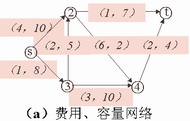
例6 给定费用、容量网络图(a),弧旁数字为(
|
||
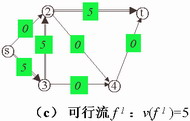
解: ⑴ 取0流为初始最小费用可行流 ⑵ 构造关于 |
||
⑶可求得W(
|
||
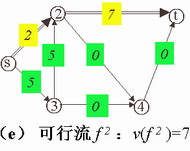
⑸可求得W(
|
||
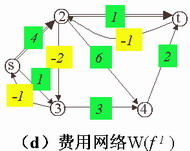
⑹构造关于
|
||
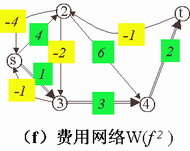
⑺可求得W(
|
||
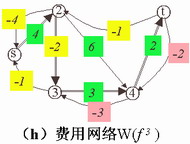
(8)构造关于
|
||
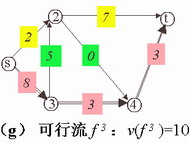
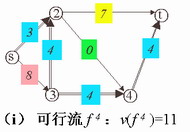
(9)可求得W(
|
||
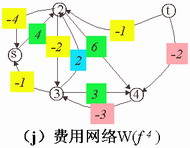
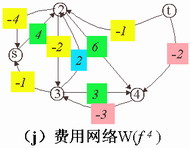
(10)构造关于
|
||
由于在W(
|
||