一、汉明码
汉明码是 1950 年由美国贝尔实验室提出来的，是第一个设计用来纠正错误的线性分组码
，汉明码及其变型已广泛应用于数字通信和数据存储系统中作为差错控制码。
在前面讨论奇偶校验时，如按偶监督，由于使用了一位监督位
，故它就能与信息位
一起构成一个代数式，如式
所示。在接收端解码时，实际上就是在计算。
当 s=0 ，就认为无错；若 s=1 ，就认为有错。上式称为监督关系式， s 称为校正子。由
于校正子 s 的取值只有这两样。它就只能代表有错 和无错这两种信息，而不能指出错码的位
置。不难推想，如果监督位增加一位，即变成两位，即能增加一个类似于
的监督关系式 。由于两个校正子的可能值四 种组合： 00 ， 01 ， 10 ， 11 ，故能表示 4 种不同信息，若用其中一个 表示无错，则其余 3 种就有可能用来指
示一位错码的 3 种不同位置。 同理， r 个监督关系式能指示一位错码的
个可能位置。
一般来说，若码长为 n ，信息位数为 k ，则监督位数 r = n - k ，如果希望用 r 个监
督位构造出 r 个监督关系式来指示一位错码的 n 种可能位置，则 要求
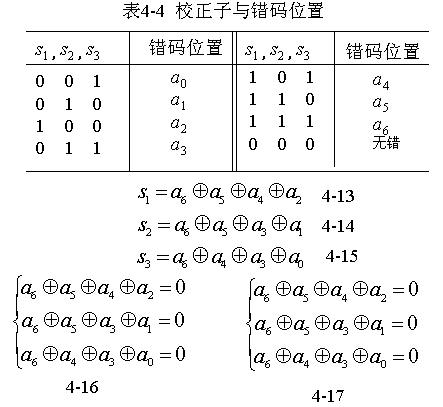
设分组码（n，k）中 k =4 。为了纠正一位错码，由式（ 4-12 ）可知，要求监督位数
，若取 r=3 ，则 n=k+r=7 。我们用
表示这 7 个码元，用
表示三个监督关系式中的校正子，则
的值与错码位置的对应关系可以规定如表 4-4 所列。
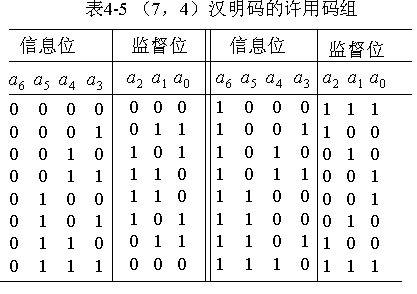
汉明码有较高的编码效率，它的效率为
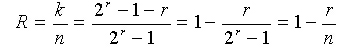
与码长相同的能纠正一位错码的其他分组码相比，汉明码的效率最高，且实现简单。因此
，至今在码组中纠正一个错码的场合还广泛地使用。当 n 很大时，则编码效率接近 1 。可见
，汉明码是一种高效码。
二、线性分组码
1 、监督矩阵
从（7，4）汉明码出发，式
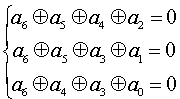就是一组线性方程例子。现将它改写成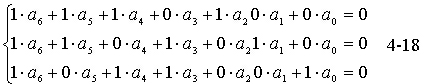
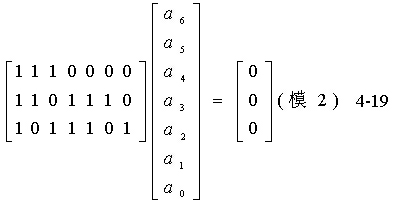
上式还可以简记为
本例中
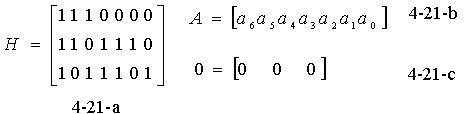
由于式（ 4-18 ）来自监督方程，因此称 H 为线性码的监督矩阵。只要监督矩阵 H 给定
，编码时监督位和信息位的关系就完全确定了。
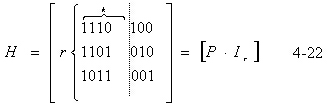
式中 P 为r×k阶矩阵， Ir 为阶单位方阵。我们将具有〔 P .Tr 〕形式 的 H 矩阵称为
典型形式的监督矩阵。
2 、生成矩阵
类似于式（ 4-16 ）改变成式（ 4-19 ）中矩阵形式那样，式（ 4- 17 ）也可以改写成
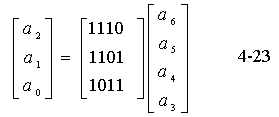
比较式（4-22）和式（4-23），可以看出式（4-23）右式前部矩阵 即为 P 。对式
（4-23）两侧作矩阵转置，得
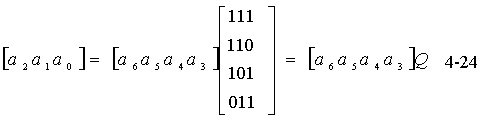
式中 Q 为一k×r阶矩阵，它为矩阵 P 的转置，即
式（ 4-24 ）表明，信息位给定后，用信息位的行矩阵乘矩阵 Q 就可计算出各监督位。
要求得整个码组，我们将 Q 的左边加上一个k×k 阶单位方阵，就构成一个新的矩阵 G ，即
G 称为生成矩阵，因为由它可以产生整个码组，即有
或者
因此，如果找到了码的生成矩阵 G ，则编码的方法就完全正确了。具有
形式的生成矩阵称为典型生成矩阵。由典型生成矩阵得 出的码组 A 中，信息位不变，监督位附加
于其后，这种码称为系统码。
比较式（4-22）和式（4-26）可见，典型监督矩阵 H 和典型矩阵 G 之间由式（ 4-25 ）
相联系。
因为又式（ 4-28 ）可以看出，任一码组 A 都是 G 的各行的线性组合。 G 的各行本身就
是一个组码。
线性代数理论还指出，非典型形式矩阵只要它的各行是线性 无关的，则可以经过运算化成
典型形式。因此，若生成矩阵是非典型形式的，则首先化成典型形式后，再用式（ 4-28 ）求
得整个组码。
3 、线性分组码主要性质
（1）封闭性
所谓封闭性，是指一种线性码中的任意两个码组之和仍为这 种码中的一个码组。若 A 1
和 A 2 是一种线性码中的两个许用码组， 则 A 1 + A 2 仍为其中的一个码组。
（2）码的最小距离等于非零码的最小重量
设（n，k ) 线性分组码仍最大检错的个数为 D ，信道的误码率为 Pe 那么，不能检错的
概率为
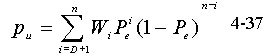
其中， Wi 重量为 I 是许用码组数目。上式证明很容易，因为错码组中，重量
的码组是不能被检测的，因此只要在的的 许可范围内求概率和即可