第二节 关系数据结构                  （1） （2） （3）
    关系模型建立在集合代数的基础上。关系数据结构的基本概念：关系，关系模式，关系数据库。
2.2.1 关系
    域是一组具有相同数据类型的值的集合。例:整数，实数，介于某个取值范围的整数，长度指定长度的
字符串集合，{‘男’，‘女’}，介于某个取值范围的日期。
1) 笛卡尔积
    给定一组域D1,D2,…,Dn，这些域中可以有相同的。D1,D2,…,Dn的笛卡尔积为：
        D1×D2×…×Dn＝｛（d1,d2,…,dn）｜di?Di，i＝1,2,…,n｝
    所有域的所有取值的一个组合，不能重复。
例： 给出三个域：
    D1=SUPERVISOR ={ 张清玫，刘逸 }
    D2=SPECIALITY={计算机专业，信息专业}
    D3=POSTGRADUATE={李勇，刘晨，王敏}
则,D1, D2, D3的笛卡尔积为：
    D1×D2×D3 ＝
    ｛ ( 张清玫，计算机专业，李勇)，(张清玫，计算机专业，刘晨)，
    ( 张清玫，计算机专业，王敏)，(张清玫，信息专业，李勇)，
    ( 张清玫，信息专业，刘晨)，(张清玫，信息专业，王敏)，
    ( 刘逸，计算机专业，李勇)，(刘逸，计算机专业，刘晨)，
    ( 刘逸，计算机专业，王敏)，(刘逸，信息专业，李勇)，
    ( 刘逸，信息专业，刘晨)，(刘逸，信息专业，王敏) ｝
2) 元组（Tuple）
    笛卡尔积中每一个元素（d1,d2,…,dn）叫作一个n元组（n-tuple）或简称元组。
3) 分量（Component）
    笛卡尔积元素（d1,d2,…,dn）中的每一个值di 叫作一个分量。
4) 基数（Cardinal number）
    若Di（i＝1,2,…,n）为有限集，其基数为mi（i＝1,2,…,n），则D1×D2×…×Dn的基数M为：
            
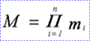
    在上例中，基数：2×2×3＝12，即D1×D2×D3共有2×2×3＝12个元组。
5)笛卡尔积的表示方法
    笛卡尔积可表示为一个二维表。表中的每行对应一个元组，表中的每列对应一个域。在上例中，12个元
组可列成一张二维表。
3. 关系（Relation）
1) 关系
    D1×D2×…×Dn的子集叫作在域D1,D2,…,Dn上的关系，表示为 R（D1, D2, … , Dn）
R：关系名
n：关系的目或度（Degree）
注意：
    关系是笛卡尔积的有限子集。无限关系在数据库系统中是无意义的。由于笛卡尔积不满足交换律，即：
    (d1,d2,…,dn )≠(d2,d1,…,dn )，但关系满足交换律，即：
    (d1,d2,…,di ,dj, … ,dn）=（d1,d2,…,dj，di ,…,dn） （i,j = 1,2,…,n）
    解决方法：为关系的每个列附加一个属性名以取消关系元组的有序性。
例 在表2.1 的笛卡尔积中取出有实际意义的元组，来构造关系：
    SAP(SUPERVISOR,SPECIALITY,POSTGRADUATE)，关系名(属性名, … ,属性名)。
假设：导师与专业：1:1，导师与研究生：1:n
于是：SAP关系可以包含三个元组：
｛ (张清玫，信息专业，李勇)，(张清玫，信息专业，刘晨)，(刘逸，信息专业，王敏) }