第二节 规范化 (1) (2) (3)
2NF的定义:若关系模式R∈1NF,并且每一个非主属性都完全函数依赖于R的码,则R∈2NF。
例:SLC(Sno, Sdept, Sloc, Cno, Grade) ∈1NF
SLC(Sno, Sdept, Sloc, Cno, Grade) ∈2NF
SC(Sno, Cno, Grade) ∈ 2NF
SL(Sno, Sdept, Sloc) ∈ 2NF
定义:关系模式 R<U,F>中若不存在这样的码X、属性组Y及非主属性A(A Y)使得X→Y,Y→A,Y→X成
立,则称 R<U,F>?3NF。结论:若 R∈3NF则每一个非主属性既不部分依赖于码也不传递依赖于码。
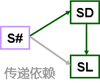
反例:关系模式 S-L(S#,SD,SL)其函数依赖有:
S#→SD,
SD→SL,
S#→SL,
若R∈3NF,则R的每一个非主属性既不部分函数依赖于候选码也不传递函数依赖于候选码。如果R∈3NF,
则R也是2NF。采用投影分解将一个2NF的关系分解为多个3NF的关系,可以在一定程度上解决原2NF关系中存
在的插入异常、删除异常、数据冗余度大、修改复杂等问题。将一个2NF关系分解为多个3NF的关系后,并不
能完全消除关系模式中的各种异常情况和数据冗余。
定义: 设关系模式R<U,F>∈1NF,如果对于R的每个函数依赖X→Y,若Y不属于X,则X必含有候选码,那
么R∈BCNF。若R∈BCNF,每一个决定属性集(因素)都包含(候选)码,R中的所有属性(主,非主属性)都
完全函数依赖于码。R∈3NF(证明),若R∈3NF 则 R不一定∈BCNF。
|


