浮点数在计算机内的格式
![]()
浮点数: X = MS ES Em-1 ...E1 E0 M-1M-2...M-n
IEEE 标准:阶码用移码,基为2
按国际电子电气工程师协会规定的国际通用标准,浮点数的阶码用整数给出,并且要用移码表示,用作为以 2为底的指数的幂。既然该指数的底一定为 2 ,可以不必在浮点数的格式中明确表示出来, 只需给出阶码的幂值即可。
移码表示只用于表示整数,只用在浮点数的阶码部分,其定义类似于整数的补码定义,差别在符号位。
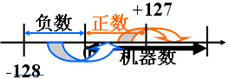
移码的符号位是 0 表示负,1 表示正,与补码的符号位正好相反,移码是指机器数在数轴上有个移位关系;
移码的数值位则与补码的数值位完全相同。
浮点数格式:关于移码的知识
![]()
浮点数: X = MS ES Em-1 ...E1 E0 M-1M-2...M-n
移码表示只用于表示整数,只用在浮点数的阶码部分。
一位符号位和 n 位数值位组成的移码, 其定义为;
[E]移 = 2n + E -2n<=E<2n 表示范围: 00000000 11111111

浮点数格式:关于移码的知识
8 位的阶码能表示-128~+127,当阶码为-128时,其移码表示为 00000000,该浮点数的绝对值<2-128,人们规定此浮点数的值为零,若尾数不为 0 就清其为 0,并特称此值为机器零。
一位符号位和 n 位数值位组成的移码, 其定义为;
[E]移 = 2n + E -2n<=E<2n 表示范围: 00000000 11111111
8 位移码表示的机器数为数的真值在数轴上向右平移了 128 个位置
移码只执行二数的加减运算与增 1、 减 1 操作。加减运算时,符号位计算结果求反后, 才是加减运算的正确符号位的值。
浮点数算术运算
浮点数加减运算
![]()
![]()
(1)对阶操作,求阶差: ΔE= MX -MY,
使阶码小的数的尾数右移│ΔE│位,
其阶码取大的阶码值;
(2)尾数加减;
(3)规格化处理;
(4)舍入操作,可能带来又一次规格化;
(5)判结果的正确性,即检查阶码上下溢出
浮点数加运算举例
X=2010*0.1101111, Y=2100*(-0.1010110)
写出X、Y的正确的浮点数表示:
阶码用 4 位移码 尾数用 8 位原码
(含符号位 ) (含符号位 )
[X]浮 = 0 1010 1101111
[Y]浮 = 1 1100 1010110
为运算方便,尾数的符号位写在数值位之前:
[MX]浮 = 1010 0 1101111
[MY]浮 = 1100 1 1010110
(1)计算阶差:
![]()
注意:阶码计算结果的符号位在此变了一次反,结果为 -2 的 移码,是X的阶码值小,使其取 Y 的阶码值1100(即 +4);
因此,相应地修改 [MX]补 =00 001101111(即右移 2 位)
(2)尾数求和:
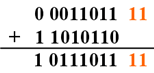
此处是原码加法,符号不相同,绝对值大的减小的,结果符号取决于绝对值大的数
(3)规格化处理:
相加结果,数值的最高位为0,应执行1次左规操作,
故得 [MX]原 = 1 1110110,阶码减1,[EX]移 = 1 011
(4)舍入处理:结果为负,警戒位为正,在最低位减 1
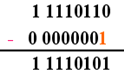
(5)检查溢出否:和的阶码为 1011,不溢出
计算后的 [X]移 = 1 1011 1110101 ,
即数的实际值为 23*(-0.1110101)
浮点数乘除运算
![]()
![]()
(1) 阶码加、减:乘:EX+EY ,除:EX- EY
(2) 尾数乘、除:乘:EX*EY ,除:EX / EY
(3) 规格化处理;
(4) 舍入操作,可能带来又一次规格化;
(5) 判结果的正确性,即检查阶码上下溢出
浮点数乘法运算举例
X=2010*0.1101111, Y=2100*(-0.1010110)
写出X、Y的正确的浮点数表示:
阶码用 4 位移码 尾数用 9 位原码
(含符号位 ) (含符号位 )
[X]浮 = 0 1010 1011
[Y]浮 = 1 1100 1101
(1)阶码相加:
![]()
注意:计算结果的阶码符号位在此变了一次反,
移码结果为 +6
(2)尾数相乘:MX*MY = 0.1011*(-0.1101)
= -0.10001111
(3) (4) (5) 已是规格化数, 不必舍入, 也不溢出
最终乘积 [MX]移 = 1 1110 10001111,
即 26 * (-0.10001111)
浮点数除运算举例
X=2010*0.1101111, Y=2100*(-0.1010110)
(1) 阶码相减:
积的阶码 = EX - EY = EX + (-EY)
= 1 010 + 0 100 = 0 110
注意:计算结果的阶码符号位在此变了一次反,为移码 -2
(2) 尾数相除:MX/MY = 0.1011/(-0.1101)
= -0.1101
(3) (4) (5) 已是规格化数, 不必舍入, 也不溢出
最终的商 [MX]移 = 1 0110 1101,
即 2-2 *(-0.1101)
IEEE 浮点数标准 754
![]()
浮点数: X = MS ES Em-1 ...E2 E1 M-1M-2...M-n
IEEE 标准:阶码用移码,基为2;尾数用原码
| 符号位 | 阶码位 | 尾数数码位 | 总位数 | |
| 短浮点数: | 1 | 8 | 23 | 32 |
| 长浮点数: | 1 | 11 | 52 | 64 |
| 临时浮点数: | 1 | 15 | 64 | 80 |
规定对长、短浮点数的尾数使用隐藏位技术,即把非 0 值的尾数的最高位上的 1 经过左移操作后强行去掉,则原来不能表示的更低一位就进到最低一位,使 23 位的尾数数值位就能给出 24 位的精度,此时还应把阶码位相应的减 1,变原来的移 128 为移 127。
正常的阶码值范围:01h~FEh,表示 -126~+127
特定的阶码:
00h,23位的非 0 尾数表示非规格化浮点数(隐藏位此时一定为0);
FFh, 尾数为全 0 时表示无穷大的浮点数,可正可负,由符号位决定。尾数非全 0 时属于非法数值