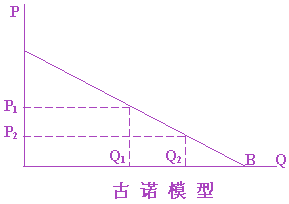
三、古诺模型
　　古诺模型假定一种产品市场只有两个卖者，并且相互间没有任何勾结行为，但相互间都知道对方将怎样行动，从而各自怎样确定最优的产量来实现利润最大化，因此，古诺模型又称为双头垄断理论。

四、斯泰克伯格模型
　　斯泰克伯格模型是一种先行者利益模型，即首先行动者在竞争中取得优势以两个寡头的竞争为例进行讨论，假设寡头所面临的需求曲线与成本状况如下所示：
　　需求函数：P=900－8Q=900－8（Q₁+Q₂）
　　平均成本与边际成本：AC=MC=100
　　R₁=（900－8Q）　　Q₁=[900－8Q₁+Q₂]Q₁=900Q₁－8Q₁²－8Q₁Q₂
　　寡头1的边际收益：MR₁=900－16Q₁－8Q₂
　　∵MR₁=MC₁ ∴900－16Q₁－8Q₂=100
　　寡头1的反应函数：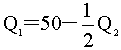
　　寡头2的反应函数：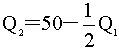
　　R₁=900Q₁－8Q₁²－8Q₁50－Q₁）=500Q₁－4Q₁²
　　MR₁=500－8Q₁
　　按MR=MC有：500－8Q₁=100
　　则有Q₁= 50
　　把Q₁=50代入寡头2的反应函数，
　　有：Q₂=50－Q₁=25
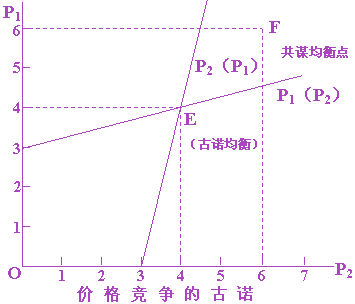
五、价格竞争的古诺模型
　　假定两个寡头分别用40元的固定成本生产可以相互替代并且有差别的产品，并假定不存在可变成本，边际成本为0，两个寡头面临的市场需求数如下：
　　D₁：Q₁=24－4P₁+2P₂
　　D₂：Q₂=24－4P₂+2P₁
　　π₁=P₁Q₁－40=24P₁－4P₁²+2P₁P₂－40
　　dπ₁/dP₁=24－8P₁+2P₂=0
　　P₁=3+1/4P₂（寡头1的反应函数）
　　同理：P₂=3+1/4P₁（寡头2的反应函数）
　　因此，P₁=4， P₂=4
　　得：Q₁=16， Q₂=16；π₁=24，π₂=24。