第一节 n阶行列式

一．数学概念

1． 逆序数

对于n个不同的元素，先规定各元素之间有一个标准次序(例如n个不同的自然数，可规定由小到大为标准次序)，于是在这n个元素的任一排列中，当某两个元素的先后次序与标准次序不同时，就说有1个逆序。一个排列中所有逆序的总数叫做这个排列的逆序数。

2． 奇排列与偶排列

逆序数为奇数的排列叫做奇排列，逆序数为偶数的排列叫做偶排列。

3． 对换

在排列中，将任意两个元素对调，其余的元素不动，这种作出新排列的手续叫做对换。将相邻两个元素对换，叫做相邻对换)

4． n阶列式

定义  设有n² 个数，排成n行n列的数表

作出表中位于不同行不同列的n个数的乘积，并冠以符号(-1) ^τ ，得到形如

的项，其中p₁,p₂,…,p_n,为自然数1,2,…,n的一个排列，为这个排列的逆序数。由于这样的排列共有n!个，因而形如上式的项共有n!项。所有这n!的代数和

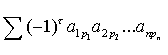
称为n阶行列式，记作

简记作det( )。数 称为行列式det( )的元素。

二．基本原理公式

定理1.1  一个排列中的任意两个元素对换，排列改变奇偶性。

推论  奇排列调成标准排列的对换次数为奇数，偶排列调成标准排列的对换次数为偶数。

定理1.2　n阶行列式也可定义为

其中t为行标排列 的逆序数。

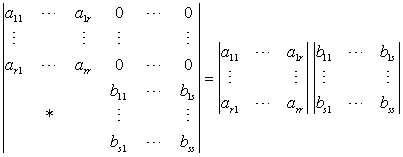
公式1　

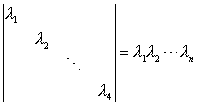
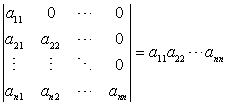
公式2

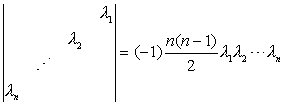
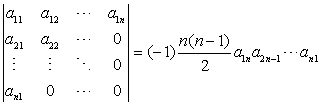
公式3　

三．重点、难点分析

逆序数的概念和n阶行列式的定义都比较抽象，难以理解。但要抓住实质，找出规律，就能透彻理解这些概念的实质。

关于求一个排列 的逆序数，它等于每个数字 的逆序之和，而对于 的逆序，可以求排列中 后面的数中比 小的数的个数，也可以求排列中 前面的数中比 大的数的个数。

关于n阶行列式，它的计算结果是一个数或者是一个多项式，而它的一般项是每一行取一个元素(而且仅仅取一个元素)，要求取在不同的列上的n个元素的乘积。把这n个元素的行标(列标)排成自然排序，其相应列标(或行标)的排列为 。它是1,2,…,n这n个数组成的全排列中的某一个n级排列。该项所带符号即是该列标(行标)排列的逆序数的奇偶性所决定的。对一般项(n!个)求和，即为行列式的值。

易见，若用行列式的定义来计算行列式是十分复杂和困难的。所以，我们用n阶行列式的定义计算出三个特殊的公式。以后可以直接用该公式计算行列式。但是如何把一个一般的行列式化成三个公式的形式，那就是下节要学的重要内容，即行列式的性质。

行列式的定义是行列式计算的基础，是学习行列式的重点。

四．典型例题分析

例1．设

，

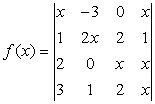则 中 的系数为_______； 的系数为_______；常数项为_______。

解：本解的解法主要是用行列式的定义，因为 是关于未知数是x的一个4次多项式，而含x⁴的项只有一项 ，含 的项有两项 和 ，常数项为 。故 的系数为2， 的系数为－10，常数项为12。