第二节 行列式的性质

一．数学概念

转置行列式

设

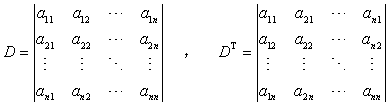
行列式D^T称为行式列D的转置行列式。

二．基本性质

性质1　行列式与它的转置行列式相等。

性质2　互换行列式的两行(列)，行列式变号。

推论　如果行列式有两行(列)完全相同，则此行列式为零。

性质3　行列式的某一行(列)中所有的元素都乘以同一数k，等于用数k乘此行列式。

推论　行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。

性质4　行列式中如果有两行(列)元素成比例，则此行列式等于零。

性质5　若行列式的某一行(列)的元素都是两数之和，例如第j列的元素都是两数之和：

             

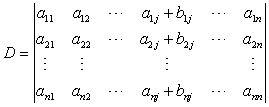
则D等于下列两个行列式之和

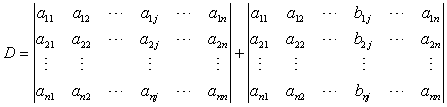
性质6　把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去，行列式不变。

三．重点，难点分析

行列式的六条基本性质是把一般的行列式变成第一节所给出的三个基本公式的钥匙，它是计算行列式必须掌握的重要理论，其难点就是如何灵活运用行列式的六条基本性质，巧妙而简捷地计算出行列式的值，掌握运算的技巧可以提高运算的速度和准确率，从而达到事半功倍的效果。

四．典型例题分析

我们知道，给出行列式的定义后，用定义直接计算行列式是比较麻烦的，例如，计算4阶行列式，用定义去计算要算24项，一个n阶的如行列式要算n!个项的代数和，但只有行列式的六条基本性质之后，就可使运算化简，从而快速计算行列式。

例2．计算

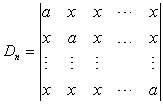
解：由于该行列式的所有列加到一起得同一个数a+(n-1)x，我们就根据这一特点，用行列式的性质6，将D_n的第2列，第3列，…，第n列的1倍同时加到第1列上去，再由性质3的推论，将公因子a+(n-1)x提出来，得

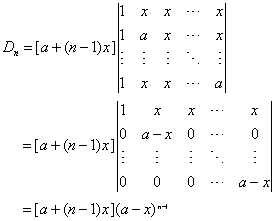
通过上面例题，我们看到主要是行列式的性质将一个行列式化成公式形式，再直接用公式的结果。这虽然比直接用定义计算简单，但是，还要经过许多步的运算才能得出结果。并且，我们在计算中还体会到计算阶数低的行列式要比阶数高的行列式简单，所以我们继续探求新的计算行列式的方法。