


第三节 行列式按行(列)展开
一.数学概念
余子式和代数余子式
在n阶行列式中,把元素
![]() 所在第i行和第j列划去后,留下来的n-1阶行列式叫做元素
所在第i行和第j列划去后,留下来的n-1阶行列式叫做元素
![]() 的余子式,记作
的余子式,记作
![]() ,记
,记
![]() ,
,
![]() 叫做元素
叫做元素
![]() 的代数余子式。
的代数余子式。
二.原理,公式
引理 一个n阶行列式,如果其中第i行所有元素除
![]() 外都为零,那么这行列式等于
外都为零,那么这行列式等于
![]() 与它的代数余子式的乘积。
与它的代数余子式的乘积。
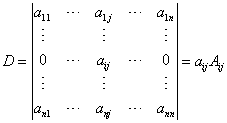
定理3.1 行列式等于它的任一行(列)的各元素与其对应的代数余子式乘积之和。即
![]()
或
![]()
推论 行列式某一行(列)的元素与另一行(列)的对应元素的代数余子式乘积之和等于零,即
![]()
![]()
![]()
范德蒙德(Vandermonde)行列式
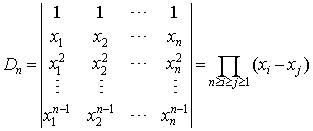
三.重点,难点分析
本节重点是行列式按行(列)展开的引理、定理、推论。灵活准确的应用行列式的性质和展开定理及其引理是快速、准确计算行列式的关键。而行列式展开定理的推论不仅告诉我们计算行列式时必须用某一行(列)的元素分别乘以该行(列)对应元素的代数余子式乘积之和时才是该行列式的值。否则乘以其它行(列)对应的元素的代数余子式的乘积之和则为零,而且该推论和展开定理并用可以计算行列式中的参数。
Vandermonde行列式虽然给出了一个计算公式,但是对于某些特殊的行列式怎么变成Vandermonde行列式的形式确是比较困难,当然用Vandermonde行列式能够计算一些难度较大的行列式的计算。
四.典型例题分析
例2.设4阶行列式的第2列元素依次为2,m,k,3,第2列元素的余子式依次为1,-1,1,-1,第4行元素的代数余子式依次为3,1,4,2,且行列式值为1,求m,k。
解:这是一道用行列式的展开定理和推论并用的计算行列式中的参数m,k的题型。由行列式的展开定理及其推论得
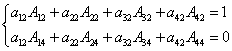
即
![]()
解得
![]()
例3.计算
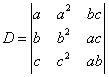
解:本题从表面上它不是Vandermonde行列式,但是我们可以用行列式的性质将其变成行列的形式,将D的第1列分别乘
![]() 加到第3列,得
加到第3列,得
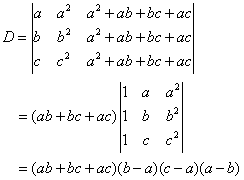
吉林大学远程教育学院©版权所有
Distant Education College, Jilin University