第四节 克拉默法则

一．数学概念

1．非齐次线性方程组

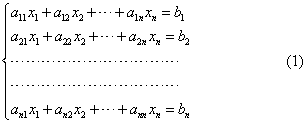
其中右端的常数项 不能全为零。

2．齐次线性方程组

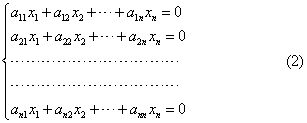
二．原理，公式和法则

克拉默法则

设非齐次线性方程组

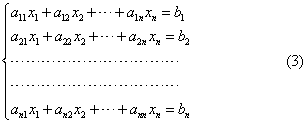
若方程组(1)的系数行列式

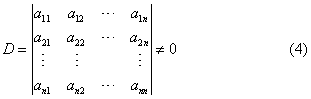
则方程组(1)有唯一解

其中 是把系数行列式D中的第j列的元素用方程组右端的常数项代替后所得到的n阶行列式，即

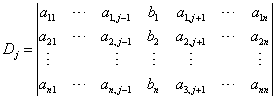
定理4.1  如果线性方程组(1)的系数行列式D≠0，则(1)一定有解，且解是唯一的。

定理4.1’  如果线性方程组(1)无解或有两个不同的解，则它的系数行列式必为零。

定理4.2  如果齐次线性方程组(2)的系数行列式D≠0，则齐次线性方程组(2)没有非零解。

定理4.2’  如果齐次线性方程组(2)有非零解，则它的系数行列式必为零。

三．重点，难点分析

我们用行列式的性质和展开定理计算各种形式的行列式，其最终目的是解未知数的个数与方程组的个数相同的线性方程组。我们要重点掌握克拉默法则，会用克拉默法则解线性方程组。在使用中注意定理4.1，4.2及其逆否定理的区别，联系和应用。

四．典型例题分析

例1．解线性方程组

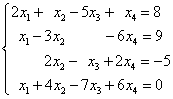
解：

      

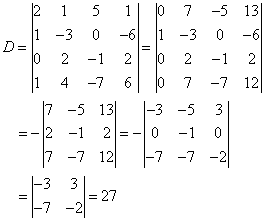
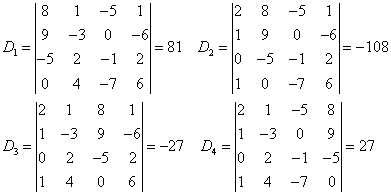
于是得

例2．问 取何值时，齐次线性方程组

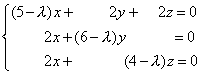
有非零解？

解：由定理4.2’可知，若齐次线性方程组有非零解，则上式的系数行列式D＝0。而

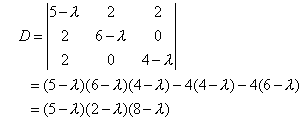
由D=0，得 =2, =5或 =8。不难验证，当 ＝2,5或8时，题给齐次线性方程组确有非零解。

本章小节

行列式的概念是基础。

行列式的性质是关键。

行列式的计算是重点。

用行列式解线性方程组是目的。