第三节　线性方程组的解

一. 数学概念

根据矩阵的乘法，可以将线性方程组写成矩阵形式。

1. n元齐次线性方程组 ；

2. n元非齐次线性方程组 ；

3. 称A为方程组的系数矩阵，B=(A，b)为非齐次线性方程组的增广矩阵。

二．原理、公式和法则

定理3.1  n元齐次线性方程组 有非零解的充分必要条件的系数矩阵A的秩

R(A)<n。

定理3.2  n元非齐次线性方程组 有解的充分必要条件的系数矩阵A的秩等于增广矩阵B=(A，b)的秩。

显然定理3.1是判断齐次线性方程组有什么样解的问题，而定理3.2是用来判断非齐次线性方程组有没有解的问题。

三. 重点、难点分析

本节的重点是会用定理3.1、3.2判定齐次线性方程组有怎样解和非齐次线性方程组有没有解。难点的如何求出方程组的解和怎样深刻理解定理3.1、3.2的证明。定理的证明虽然简单明了，但用前面已学过的许多知识，并且方法独特，不易掌握和理解。

四. 典型例题

例1 求解齐次线性方程组

 

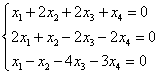
解：对系数矩阵A施行初等行变换为行最简形矩阵：

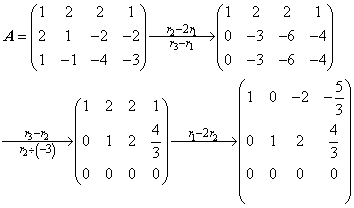
即得与方程组同解的方程组

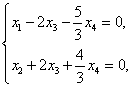
由此即得

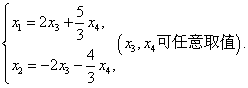
令 ，把它写成通常的参数形式

   

其中 为任意实数，或写成向量形式

 

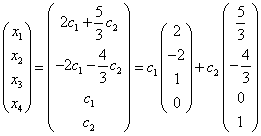
例2. 设有线性方程组

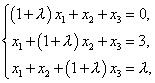
问 取何值时，此方程组(1)有唯一解；(2)无解；(3)有无限多个解？并在有无限多解时求其通解。

解：对增广矩阵B=(A，b)作初等行变换把它变为行阶梯形矩阵，有

     

当 时，R(A)= R(B)=3，方程组有唯一解；

当 时，R(A)=1， R(B)=2，方程组无解；

当 时，R(A)= R(B)=2，方程组有无限多个解，

当 时，

   

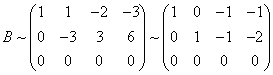
由此便得通解

   

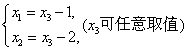
即

    

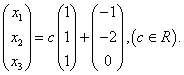
通过上面的实例，我们可知对于齐次线性方程组，只须把它的系数矩阵化为行最简形矩阵，找出与原方程组等价的线性方程组，便能写出通解。对于非齐次线性方程组，只须把它  增广矩阵化成行列阶梯矩阵，便能根据定理3.2判断它是否有解；在有解时，把增广矩阵进一步化成最简形矩阵，从而写出它的通解。