第四节 初等方阵

一. 数学概念

定义4.1  由单位矩阵E经过一次初等变换得到的矩阵称为初等方阵。

1. 对调单位矩阵的两行(列)，得E[i，j];

2. 以数 乘某行或某列，得E[i(k)]  ;

3. 以数k乘某行(列)加到另一行(列)上去，得E[i，j(k)].

4. 初等方阵均为可逆的方阵，其逆仍是同种的初等方阵。

二. 原理公式和法则

定理4.1  设A是一个 矩阵对A施行一次初等行变换，相当于在A是左边乘以相应的m阶初等矩阵；对A施行一次初等列变换，相当于在A右边乘以相应的n阶初等方阵。

定理4.2  设A为可逆矩阵，则存在有限个初等矩阵 。

推论     矩阵A~B的充分必要条件是：存在m阶可逆矩阵P及n阶可逆矩阵Q使PAQ=B。

求逆公式

          

求 的公式

             

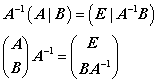
三. 重点、难点分析

本节的重点是用初等变换求可逆矩阵的逆矩阵。难点是用初等变换求可逆矩阵的逆矩阵的方法与技巧，以上面公式的推导。

四. 典型例题

例1设

。

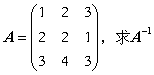  解：

  。

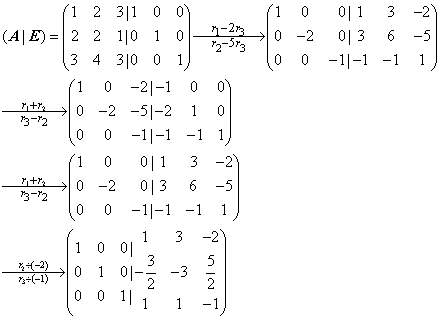
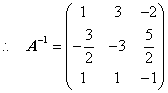利用初等行变换求可逆矩阵的方法，还可用于求矩阵 。由

可知，若对(A|B)施行初等行变换，当把A变成E时，B就变成 。

例2. 求矩阵X，使AX=B，其中

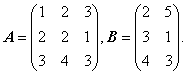
解：若A可逆，则 .

 

因此

  。

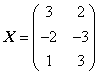本例用初等行变换的方法求得 ，如果要求 ，则可对矩阵 作初等列变换，使

，

即可得 。不过通常都习惯作初等行变换，那末可改为对 作初等行变换，使

，

即可得 ，从而求得Y。