第四节 线性方程组解的结构

一．数学概念

1. 齐次线性方程组

Ax=0

2. 非齐次线性方程组

  Ax=b   （b ≠ 0）

3. 齐次线性方程组的基础解系

是Ax=0的解，满足

(i) 线性无关；

(ii) Ax=0的任何一解都可由 线性表示。

4. 齐次线性方程组Ax=0的通解

        

5. 非齐次线性方程组Ax=b的通解

  

二．原理，公式和法则

1. n个未知数的齐次方程组Ax=0有非零解的充分必要条件是R(A)<n。

2. n个未知数的非齐次线性方程组Ax=b有解的充分必要提哦案件是系数矩阵A的秩等于增广矩阵B的秩。且当R(A)=R(B)=n时，方程组有唯一解，当R(A)=R(B)=r<n时方程组有无穷多个解。

3. 若 ， 为Ax=0的解，则 也是Ax=0的解。

4. 若 是Ax=0的解， ，则 的解。

5. 若 ， 是Ax=b的两个解，则 是Ax=0的解。

6. 若 是Ax=0的解， 是Ax=b的解，则 是Ax=b的解。

7. n元齐次线性方程组 的全体解所构成的集合S的一个向量空间，当系数矩阵的秩R(A)=r时，解空间是n-r维的。

三．重点，难点分析

本节的重点是讨论线性方程组解的结构；齐次线性方程组Ax=0解与其对应的非齐次线性方程组Ax=b的解之间的关系；如何求齐次线性方程组和非齐次线性方程组的通解；真正理解向量组的线性相关性与其所对应的齐次线性方程组有什么样解的关系；一个向量是否能由一组向量线性表示与其对应的非齐次线性方程组是否有解的关系。难点是如何理解这些关系，和正确解出齐次线性方程组和非齐次线性方程组的通解。

四．典型例题

例1.设线性方程组

 

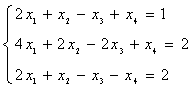
求出方程组的通解；

写出非齐次线性方程组所对应的齐次线性方程组的基础解系；

写出非齐次线性方程组的一个特解。

解：对方程组的增广矩阵B施行初等行变换得       

显然R(A)=R(B)=2<4，所以原方程组有无穷多解，且等价与下面方程组

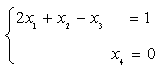
解得

 

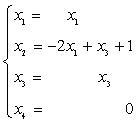
故方程组的通解为

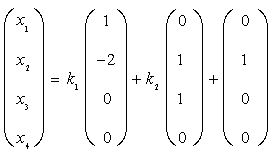
     为任意常数

该方程组所对应的齐次线性方程组的基础解系为

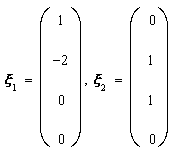
该方程组的一个特解为

  

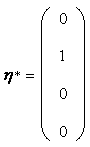
解此类题的方法是先对方程组的增广矩阵施行初等变换，使之变成最简型矩阵中首非零元1为系数的未知数留在等号的左边作为非自由的未知量(其个数等于R(A)，其余的未知量移到等号右边作为自由未知量，其个数等于方程组所对应的齐次线性方程组的基础解系中解向量的个数)。根据通解的结构，得出方程组的通解。

例2．设向量组

   

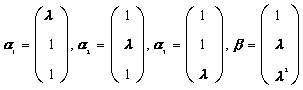
试问(1)当 为何值时，β能由 线性表示，且表示法唯一？

(2)当 为何值时，β不能由 线性表示？

(3)当 为何值时，β能由 线性表示，且表示法不唯一，并写出表示试。

解：设 ，使

  

由于                                

 

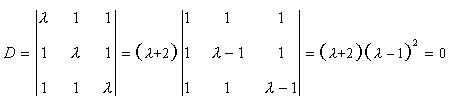
①当 时，β能由 线性表示，且表示法唯一。

②当 时

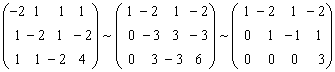
显然R(A)=2，R(B)=3，方程组无解，即B不能由 线性表示。

③当 时                                   

  

     

显然R(A)= R(B)=1<3，方程组有无穷多解。

   

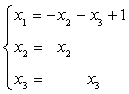
即

     

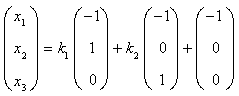
为任意常数

故β能由 线性表示，且

             为任意常数

此类问题将线性表示问题转化非齐次线性方程组求解问题，按有唯一解、无解和有无穷多解说明β能由 唯一的线性表示，不能表示，有无穷多组表示法等。