第一节  向量的内积

一．数学概念

1. 内积：设有n维向量

         

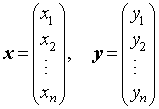
令        ，

则称[x,y]为向量x与y的内积。

2. 范数：称 为向量x的范数(或长度)。

3. 单位向量：称 时的向量x为单位向量。

4. 当 ， 时，称

           

为向量x与y的夹角。

5. 正交向量组：指一组两两正交的单位向量。

6. 标准正交基：设n维向量 是向量空间V的一个基，如果 两两正交，且都是单位向量，则称 是V的一个标准正交基。

7. 正交矩阵：如果n阶方阵A满足

                      

那末称A为正交矩阵。

8. 正交变换：若P为正交矩阵，则线性变换x=Py称为正交变换。

二．原理，公式和法则

1 .内积的结果是一个数(或是一个多项式)，且满足如下性质(其中x,y,z为n维向量， 为实数)：

  (i) ；

  (ii) ；

  (iii)

2 .向量的范数是一个数，且满足如下性质：

(i) 非负性  当x ≠ 0时, ；当x = 0时, 。

(ii) 齐次性   ；

(iii) 三角不等式  。

3. 是单位向量。

4. 正交向量组是线性无关的。

5. 施密特标准正交化

设 线性无关，

取 ,                              令

                    

           

……………………………………………………

   

三 .重点、难点分析

本节主要讲述一些预备知识，其重点是向量的内积，范数，标准正交基，正交矩阵及正交变换，会够造正交矩阵，易得正交变换，正交变换是在下面的学习中经常要用到的，难点是施密特标准正交化。

四 .典型例题

例1 .已知向量 ，求一组非零向量a₁,a₂，使a₁与a₂,a₃正交，并把a₁,a₂,a₃化成R³的一个标准正交基。

解：设所求的向量x,是[a₃,x] = 0，即

，

它的基础解系为

，

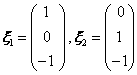令

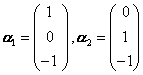，把它们标准正交化，

，                       

，

， ,

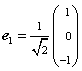
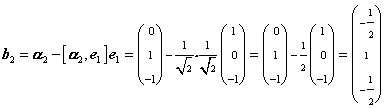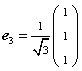显然 是两两正交的单位向量，故 是 的一个标准正交基。

   

解本题关键在与所求向量与已知向量正交，由它们的内积等于零，得出齐次线性方程组，其基础解系即为所求的向量，然后再把已知的3个向量施密特标准化。