第六节 正定二次型

一．数学概念

1 .正定二次型

设有实二次型 ，如果对任何x≠0都有f(x)>0(显然f(0)=0)，则称f为正定二次型，并称矩阵A是正定的，记之A>0.

2 .负定二次型

对于实二次型 ，如果对任何x≠0都有f(x)<0，则称f为负二次型，并称矩阵A是负的，记之A<0.

二.原理，公式和法则

惯性定律

设有实二次型 ，它的旨为r，有两个实可逆变换

x=Cy，及x=Pz

使

及

则 中正数的个数相等。

正定二次型的判定

实二次型 为正定的充分必要条件是：它的标准形的n个系数全为正。

正定矩阵的判定

对称矩阵A为正定的充分必要条件是：A的特征值全为正。 

对称矩阵A为正定的充分必要条件是：A的各阶顺次主子式都为正。即

 _。

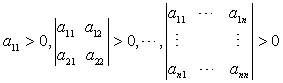负定矩阵的判定

对称矩阵A为负定矩阵的充分必要条件的：奇数阶主子式为负，而偶数阶主子式为正。即

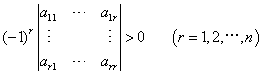
三 .重点、难点分析

本节的重点是判定二次型的正定性，理解正定二次型的实际意义，难点是正定二次型正定性判定定理的证明及其二次型正定性的证明。

四 .典型例题

当 为何值时，二次型

为正定二次型？

解：二次型f的矩阵A为

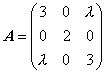
由于3>0，

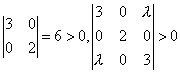
即

故当 时，f为正定二次型。

由于二次型f与对称矩阵是一一对应的关系，要证二次型正定，则可证明其对应的对称矩阵正定；反之若要证明对称矩阵为正定矩阵，也只须正它所对应的二次型为正定二次型。

例2 .设 矩阵，若R(A)=n，则A^TA为正定矩阵。

证：因为 ，所以A^TA为对称矩阵，又因R(A)=n，那么，对任何n维列向量x≠0，则 ，于是

故 为正定二次型，因此A^TA为正定矩阵。

例3 .设3阶实对称矩阵A满足 ，且R(A)=2，(1)写出 在正交变换下的标准形；(2)判定 的正定性；(3)求在||x||=1时f的最大值和最小值。

解：设 是A的特征值，x是A的关于特征值 所对应的特征向量，从而 ，

由已知 ，而x≠0，所以

由于R(A)=2，所以 是A的3个特征值。

又A+E仍是实对称矩阵，且特征值为3，3，1，从而在正交变换下的标准形

(1)

(2) 由于f的标准形的系数全为正，故f为正定二次型。

(3) 由于

 

即1≦f≦3     故当||x||=1时，f的最大值为3，最小值为1。