 |
| 液体和气体与固体不同,它们没有固定的形状,各部分之间的作用力很小,容易产生相对运动,具有流动性,故将它们统称为流体。研究静止流体的力学称为流体静力学,研究运动流体的力学称为流体动力学,两者合称为流体力学。流体的运动广泛存在于我们的周围以及动植物体内,了解它的运动规律,对于研究人体血液循环和呼吸过程是十分重要的。本章将讨论流体的一些基本概念和规律,并针对血液在人体中的流动特点展开讨论。 |
|
 |
 |
• 重点掌握理想流体的连续性方程和伯努利方程,黏性流体的泊肃叶定律的物理意义并能熟练应用;
• 确切理解理想流体与黏性流体,稳定流动与层流、黏度、雷诺数、外周阻力、血沉等概念,黏性流体伯努利方程、牛顿黏性定律、斯托克斯黏性公式在血液流动过程中的应用;
• 了解心脏做功,血流速度及血管中血压的分布。
|
|
 |
|
| 知识点十 泊肃叶定律 |
|
物理表达:法国医学家泊肃叶研究了血管中血液的流动,并对在压强差作用下,在长度为 L 的细玻璃管中流体的流动进行了研究,发现不可压缩黏性液体在圆管中定常流动时,通过圆管两端的压强差成正比、与管半径的四次方成正比、与管长成反比。
数学表达:
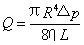
例题 1 :利用泊肃叶定律导出医学上外周阻力的表达式
解:我们将泊肃叶定律表达成另一种形式:
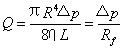
其中
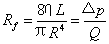 , ,
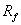 称为流阻。 称为流阻。
若 L 表示血管从左心室到右心房的总长度,这时的 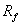 称为外周阻力。 称为外周阻力。
由于,左心室和右心房的平均压强之差为:Δ p= 舒张压 + (收缩压-舒张压) /3
Q= 心脏每搏血量×心率 /60s ,则外周阻力可表示为:

|
|
|

