 |
| 物体在一定位置附近做来回往复的运动,称为振动。振动是自然界中广泛存在的一种现象,如钟摆的运动、气缸活塞的运动等。这些振动中物体的位置是随时间的变化的,因此又称为机械振动。振动现象并不仅限于力学中的机械振动,在物理学的其他领域中也存在与机械振动类似的振动现象。一般的,任何一个物理量在某一定值附近做反复的变化,都可以称为振动。例如,交流电中电流和电压的反复变化,就是这种现象。振动的传播过程称为波动。在弹性介质中产生的波动,是靠弹性介质质点的机械振动产生和传播的,又称为机械波,水面波和声波都是机械波。光波、无线电波、X射线等可以在真空中传播,并不依赖于弹性介质,这类波称为电磁波。机械波和电磁波在本质上不同,但是都具有波动的共同特性,服从相似的规律。本章先讨论简谐振动的基本规律,然后介绍波动的现象和规律。 |
|
 |
 |
• 重点掌握简谐振动方程、波动方程及其物理意义;
• 确切理解简谐振动的合成、波的干涉现象及其规律;
• 了解驻波的形式及其规律。
|
|
 |
|
| 知识点五 旋转矢量表示法 |
|
简谐振动的位移与时间的关系可以用几何方法表示,这种方法称为旋转矢量表示法。对于给定的简谐振动 x=Acos(ωt+φ),可以将它看做矢量A在x轴上的投影,在取定的x轴上任选一原点O做平衡位置,自O点做一矢量A,其长度等于振幅A,矢量A称为振幅矢量。先令A与x轴的夹角等于初相位φ,若A在t=0时从该位置以角频率ω相同的匀角速度在平面内沿逆时针方向转动,则在任意时刻t,矢量A与x轴的夹角ωt+φ就是该时刻的相位。显然,旋转矢量A在x轴上的投影Acos(ωt+φ)表示了给定的简谐振动,或者说,矢量A的末端在x轴上的投影点P沿x轴做简谐振动。由简谐振动的旋转矢量表示法可以看出,矢量A转动一周,相当于简谐振子振动一个周期。即往返运动一次。ωt+φ从0到2π的变化过程中,表示出了一个周期中简谐振子的各个不同位置。
点击观看旋转矢量动画
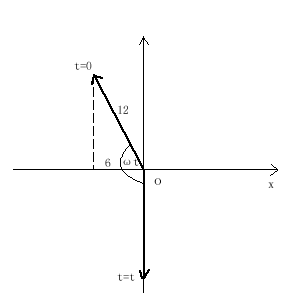
例题 1 物体的振动方程为x=12cos(πt-π/3)cm,求此物体由x=-6cm处向x轴负方向运动并回到平衡位置所需要的时间。
解:本题用旋转矢量表示法求解较为简单。画出题给的振子初、末状态位置,如图,它们之间的角度即为ω t = arcos(6/12) + π/2 =π/3 + π/2 = 5π/6
所以: t = 5π/6ω = 5π/6π = 5/6 (s)
|
|
|

