第四节 关系代数 (1) (2) (3) (4) (5) (6)
2. 投影(Projection)
1)投影运算符的含义:从R中选择出若干属性列组成新的关系,πA(R) = { t[A] | t∈R }, A:R中的
属性列。
2)投影操作主要是从列的角度进行运算:

但投影之后不仅取消了原关系中的某些列,而且还可能取消某些元组(避免重复行)。
[例3] 查询学生的姓名和所在系, 即求Student关系上学生姓名和所在系两个属性上的投影:
πSname,Sdept(Student) 或 π2,5(Student)
结果:
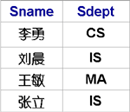
[例4] 查询学生关系Student中都有哪些系:πSdept(Student),结果:

3. 连接(Join)
1)连接也称为θ连接;
2)连接运算的含义:从两个关系的笛卡尔积中选取属性间满足一定条件的元组:
R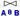 S = { S = { |tr∈R∧ts∈S∧tr[A]θts[B]},A和B:分别为R和S上度数相等且可比的属性组;θ: |tr∈R∧ts∈S∧tr[A]θts[B]},A和B:分别为R和S上度数相等且可比的属性组;θ:
比较运算符。连接运算从R和S的广义笛卡尔积R×S中选取(R关系)在A属性组上的值与(S关系)在B属性组
上值满足比较关系的元组。
3)两类常用连接运算
等值连接(equijoin)——θ为“=”的连接运算称为等值连接。从关系R与S的广义笛卡尔积中选取A、B属
性值相等的那些元组,即等值连接为:
R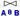 S = { S = { |tr∈R∧ts∈S∧tr[A] = ts[B] } 。 |tr∈R∧ts∈S∧tr[A] = ts[B] } 。
自然连接(Natural join)——是一种特殊的等值连接,两个关系中进行比较的分量必须是相同的属性组。
在结果中把重复的属性列去掉,R和S具有相同的属性组B:
R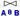 S = { S = { |tr∈R∧ts∈S∧tr[B] = ts[B] }。 |tr∈R∧ts∈S∧tr[B] = ts[B] }。
4)一般的连接操作是从行的角度进行运算。
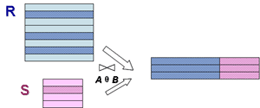
自然连接还需要取消重复列,所以是同时从行和列的角度进行运算。
|


