第四节 关系代数 (1) (2) (3) (4) (5) (6)
5)
[例5]
4)象集Z
给定一个关系R(X,Z),X和Z为属性组。当t[X]=x时,x在R中的象集(Images Set)为:
Zx={ t[Z]|t∈R,t[X]=x },它表示R中属性组X上值为x的诸元组在Z上分量的集合。
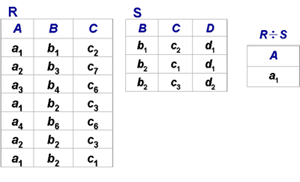
4. 除(Division)——给定关系R (X,Y) 和S (Y,Z),其中X,Y,Z为属性组。R中的Y与S中的Y可以有不同的
属性名,但必须出自相同的域集。R与S的除运算得到一个新的关系P(X),P是R中满足下列条件的元组在X属
性列上的投影:元组在X上分量值x的象集Yx包含S在Y上投影的集合。
R÷S = {tr [X] | tr∈R∧πY (S)∈Yx }
Yx:x在R中的象集,x = tr[X]
2)除操作是同时从行和列角度进行运算:
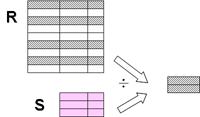
3)
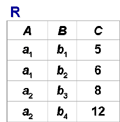
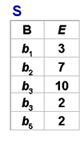
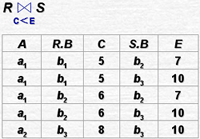
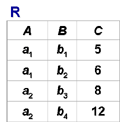
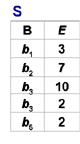
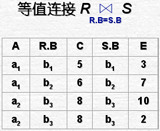
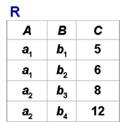
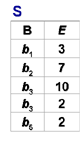
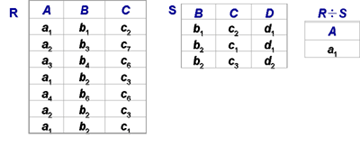
[例6] (p62)在关系R中,A可以取四个值{a1,a2,a3,a4},a1的象集为 {(b1,c2),(b2,c3),(b2,c1)},a2的
象集为 {(b3,c7),(b2,c3)},a3的象集为 {(b4,c6)},a4的象集为 {(b6,c6)},S在(B,C)上的投影为{(b1,c2),(b2,c1),(b2,c3) },只有a1的象集包含了S在(B,C)属性组上的投影,R÷S ={a1}:
|


