


第二节 逆矩阵
一. 数学概念
定义2.1 设A为n阶方阵,若存在一个n阶方阵B使
![]() ,则称矩阵A是可逆的,并把矩阵称为A的逆矩阵。
,则称矩阵A是可逆的,并把矩阵称为A的逆矩阵。
1. 可逆矩阵又称为非奇异矩阵。
2. 不可逆矩阵又称为奇异矩阵。
二. 原理,公式和法则
1. 定理2.1 方阵A可逆的充分必要条件是
![]() ,且
,且
![]() ,其中
,其中
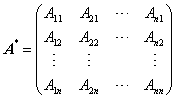
为A的伴随矩阵。
推论 若AB=E(或BA=E)则B=A-1。
性质 逆矩阵是唯一的。
2. 运算律
① 若A可逆,则A-1亦可逆,且
![]() 。
。
② 若A可逆,数
![]() ,则λA可逆,且
,则λA可逆,且
![]() 。
。
③ 若A,B为同阶矩阵且均可逆,则AB亦可逆,且
![]()
④ 若A可逆,则AT亦可逆,且
![]()
三. 重点,难点分析
可逆矩阵的求逆既是本节的重点,也是本节的难点,它也是本章的重点。这是因为求逆矩阵它不仅可以解n个方程n个未知数方程组的求解,也可以解矩阵方程,而且在今后的学习中还要经常遇到求逆矩阵的计算。由关系式求逆和抽象矩阵的求逆对初学者来说是比较困难的。
四. 典型例题
例1. 设A为n阶方阵,若
![]() ,试证A-E可逆,并求x。
,试证A-E可逆,并求x。
证明 由
![]() ,得
,得
![]() ,在此两端同加单位矩阵得
,在此两端同加单位矩阵得
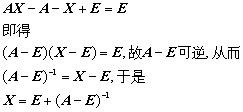
例2. 设
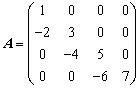
E为4阶单位矩阵,且
![]() ,求
,求
![]() 。
。
解:在
![]() 的两边左乘(E+A)得,
的两边左乘(E+A)得,
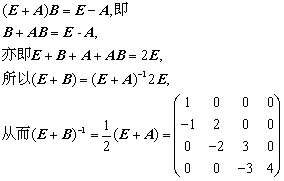
例3. 设矩阵A的伴随矩阵
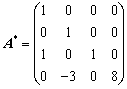 ,
,
且
![]() ,其中E为4阶单位矩阵,求B。
,其中E为4阶单位矩阵,求B。
解:在
![]() 左乘A*,右乘A得
左乘A*,右乘A得
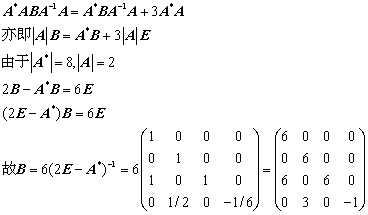
吉林大学远程教育学院©版权所有
Distant Education College, Jilin University